Giải bài 9 trang 106 vở thực hành Toán 9 tập 2
Cho tam giác ABC và O là trung điểm của cạnh AB. a) Tìm một phép quay tâm O biến điểm A thành điểm B và biến điểm B thành điểm A. b) Phép quay trên biến điểm C thành điểm D. Hãy chứng tỏ rằng ACBD là một hình bình hành.
Đề bài
Cho tam giác ABC và O là trung điểm của cạnh AB.
a) Tìm một phép quay tâm O biến điểm A thành điểm B và biến điểm B thành điểm A.
b) Phép quay trên biến điểm C thành điểm D. Hãy chứng tỏ rằng ACBD là một hình bình hành.
Phương pháp giải - Xem chi tiết
a) Phép quay ngược chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
b) Chứng minh AB và CD cắt nhau tại trung điểm O của mỗi đoạn nên ACBD là hình bình hành.
Lời giải chi tiết
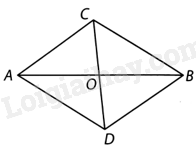
a) Phép quay ngược chiều \({180^o}\) tâm O biến A thành B và biến B thành A.
b) Nếu phép quay trên biến C thành D thì C và D; A và B đối xứng với nhau qua O.
Do đó hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn.
Do đó ACBD là hình bình hành.