Giải bài tập 10.33 trang 133 SGK Toán 9 tập 2 - Cùng khám phá
Đài truyền hình điều tra ý kiến của một số khán giả về một chương trình giải trí. Kết quả điều tra được thống kê trong bảng bên. Chọn ngẫu nhiên một trong số những người được điều tra. Tính xác suất của các biến cố: a) A: “Chọn được 1 khán giả nữ không thích chương trình” b) B: “Chọn được 1 khán giả nam” c) C: “Chọn được 1 khán giả thích chương trình”.
Đề bài
Đài truyền hình điều tra ý kiến của một số khán giả về một chương trình giải trí. Kết quả điều tra được thống kê trong bảng bên.
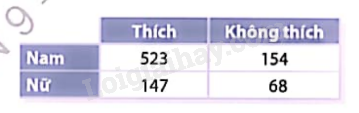
Chọn ngẫu nhiên một trong số những người được điều tra. Tính xác suất của các biến cố:
a) A: “Chọn được 1 khán giả nữ không thích chương trình”
b) B: “Chọn được 1 khán giả nam”
c) C: “Chọn được 1 khán giả thích chương trình”.
Phương pháp giải - Xem chi tiết
Cho A là một biến cố liên quan đến phép thử T. Nếu phép thử T có n kết quả đồng khả năng xảy ra, trong đó có k kết quả thuận lợi cho biến cố A, thì xác suất của biến cố A được tính theo công thức: \(P(A) = \frac{k}{n}\) .
Lời giải chi tiết
Chọn ngẫu nhiên một trong 892 người được điều tra nên không gian mẫu có 892 kết quả có thể xảy ra.
a) Biến cố A: “Chọn được 1 khán giả nữ không thích chương trình” có 68 kết quả thuận lợi.
Suy ra \(P(A) = \frac{{68}}{{892}} = \frac{{17}}{{223}}\) .
b) Biến cố B: “Chọn được 1 khán giả nam” có 677 kết quả thuận lợi.
Suy ra \(P(B) = \frac{{677}}{{892}}\) .
c) Biến cố C: “Chọn được 1 khán giả thích chương trình” có 670 kết quả thuận lợi.
Suy ra \(P(C) = \frac{{670}}{{892}} = \frac{{335}}{{446}}\) .