Giải bài tập 3. 14 trang 105 SGK Toán 12 tập 1 - Cùng khám phá — Không quảng cáo

Đề bài

Hai bảng dưới đây trình bày kết quả thống kê lượng cà phê (tính theo cm³) được pha chế trong mỗi cốc do hai máy bán cà phê tự động A và B thực hiện trong một ngày:

a) Ước tính giá trị trung bình và độ lệch chuẩn của lượng cà phê trong những cốc được pha chế bởi:

- Máy A.

- Máy B.

b) Giả sử lượng cà phê mong muốn trong mỗi cốc là 250 cm³. Nếu định kinh doanh cà phê bằng hình thức bán hàng tự động thì anh Hùng nên chọn mua loại máy nào?

Lời giải chi tiết

a) Bảng phân phối tần số cho máy A và B:

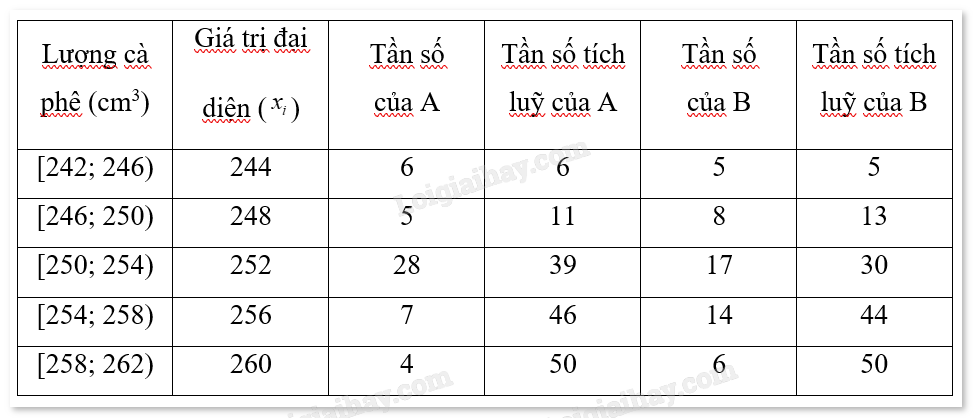
Dựa vào bảng phân phối ta thấy N = 50

Giá trị trung bình của máy A:

${\bar x_A} = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}}  \times {x_i} = \frac{{6 \times 244 + 5 \times 248 + 28 \times 252 + 7 \times 256 + 4 \times 260}}{{50}} = 251,84$

Độ lệch chuẩn của máy A:

${S_A} = \sqrt {\overline {x_A^2}  - {{\left( {{{\bar x}_A}} \right)}^2}}$

$\overline {x_A^2}  = \frac{{\sum {{f_i}x_i^2} }}{N} = \frac{{6 \times {{244}^2} + 5 \times {{248}^2} + 28 \times {{252}^2} + 7 \times {{256}^2} + 4 \times {{260}^2}}}{{50}} = \frac{{3172000}}{{50}} = 63440$

\){S_A} = \sqrt {63440 - 251,{{84}^2}}  = \sqrt {16,6144}  \approx 4,076\)

Giá trị trung bình của máy B:

${\bar x_B} = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}}  \times {x_i} = \frac{{5 \times 244 + 8 \times 248 + 17 \times 252 + 14 \times 256 + 6 \times 260}}{{50}} = 252,64$

Độ lệch chuẩn của máy B:

${S_B} = \sqrt {\overline {x_B^2}  - {{\left( {{{\bar x}_B}} \right)}^2}}$

$\overline {x_B^2}  = \frac{{\sum {{f_i}x_i^2} }}{N} = \frac{{5 \times {{244}^2} + 8 \times {{248}^2} + 17 \times {{252}^2} + 14 \times {{256}^2} + 6 \times {{260}^2}}}{{50}} = \frac{{3192384}}{{50}} = 63847,68$

${S_B} = \sqrt {63848,68 - 252,{{64}^2}}  = \sqrt {20,7104}  \approx 4,55$

b)

Sau khi tính toán, anh Hùng nên chọn máy A vì máy A có giá trị trung bình gần với 250 cm³ nhất và có độ lệch chuẩn nhỏ nhất.