Giải bài tập 4.19 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức
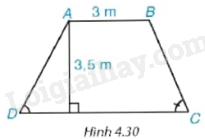
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30) . Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là (tan D = 1,25.) Độ dốc của sườn BC, tức là (tan C = 1,5.) Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm) .
Đề bài
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30) . Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là \(\tan D = 1,25.\) Độ dốc của sườn BC, tức là \(\tan C = 1,5.\) Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).
Phương pháp giải - Xem chi tiết
Gọi H là chân đường vuông góc kẻ từ A, ta mới tính được cạnh AD và DH dựa theo tỉ số lượng giác, chưa đủ để tính cạnh DC và BC, do đó ta kẻ thêm đường cao BK của hình thang, ta sẽ có ABKH là hình chữ nhật, ta tính được cạnh HK, tam giác BCK tính được BC và CK. Để tính DC ta tổng độ dài 3 cạnh DH, HK, KC. Chú ý làm tròn đến đơn vị dm tức là phần thập phân lấy 1 chữ số.
Lời giải chi tiết
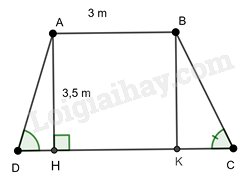
Kẻ BK vuông góc với DC tại K và AH vuông góc với DC tại H nên hình thang có hai đường cao là AH và BK; AB= BK = 3,5 m
Xét tứ giác ABKH có AH // BK; AH = BK; \(\widehat {AHK} = {90^0}\)
Nên ABKH là hình chữ nhật suy ra HK = AB = 3 m
Tam giác ADH vuông tại H nên ta có:
\(\tan \widehat D = \frac{{AH}}{{DH}}\) hay \(1,25 = \frac{{3,5}}{{DH}}\) suy ra \(DH = \frac{{3,5}}{{1,25}} = 2,8\) m = 28 dm.
\(A{D^2} = D{H^2} + A{H^2} = 3,{5^2} + 2,{8^2} = 20,09\) hay \(AD = \sqrt {20,09} \approx 4,5\) m = 45 dm (vì \(AD > 0\))
Tam giác BKC vuông tại K nên ta có:
\(\tan \widehat C = \frac{{BK}}{{KC}}\) hay \(1,5 = \frac{{3,5}}{{KC}}\) suy ra \(KC = \frac{{3,5}}{{1,5}} = \frac{7}{3} \approx 2,3\) m = 23 dm.
\(B{C^2} = B{K^2} + K{C^2} = 3,{5^2} + 2,{3^2} = 17,54\) hay \(BC = \sqrt {17,54} \approx 4,2\) m =42 dm (vì \(BC > 0\))
Độ dài cạnh DC là \(DC = DH + HK + KC \approx 2,8 + 3 + 2,3 = 8,1m \approx 81dm\)