Giải bài tập 5 trang 117 SGK Toán 9 tập 1 - Cánh diều
Cho hai đường tròn (left( O right),left( I right)) cắt nhau tại hai điểm (A,B). Kẻ các đoạn thẳng (AC,AD) lần lượt là đường kính của hai đường tròn (left( O right),left( I right)). Chứng minh ba điểm (B,C,D) thẳng hàng.
Đề bài
Cho hai đường tròn \(\left( O \right),\left( I \right)\) cắt nhau tại hai điểm \(A,B\). Kẻ các đoạn thẳng \(AC,AD\) lần lượt là đường kính của hai đường tròn \(\left( O \right),\left( I \right)\). Chứng minh ba điểm \(B,C,D\) thẳng hàng.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất số đo góc nội tiếp để chứng minh.
Lời giải chi tiết
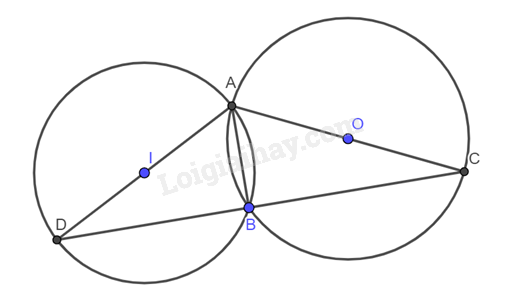
Xét đường tròn \(\left( I \right)\) có: \(\widehat {ABD}\) là góc nội tiếp chắn nửa đường tròn.
Vậy \(\widehat {ABD} = 90^\circ \).
Xét đường tròn \(\left( O \right)\) có: \(\widehat {ABC}\) là góc nội tiếp chắn nửa đường tròn.
Vậy \(\widehat {ABC} = 90^\circ \).
Ta có: \(\widehat {ABD} + \widehat {ABC} = 90^\circ + 90^\circ \Rightarrow \widehat {BDC} = 180^\circ \).
Vậy ba điểm \(B,D,C\) thẳng hàng.