Giải bài tập 9.26 trang 89 SGK Toán 9 tập 2 - Kết nối tri thức
Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2cm. Tính độ dài các cạnh của tam giác ABC.
Đề bài
Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2cm. Tính độ dài các cạnh của tam giác ABC.
Phương pháp giải - Xem chi tiết
+ Vì tam giác ABC đều nội tiếp đường tròn (O) nên O là trọng tâm, trực tâm của tam giác ABC.
+ Gọi H là giao điểm của AO và BC nên AH là trung trực đồng thời là đường cao trong tam giác đều ABC. Do đó: \(OA = \frac{{BC\sqrt 3 }}{3}\), từ đó tính được BC.
Lời giải chi tiết
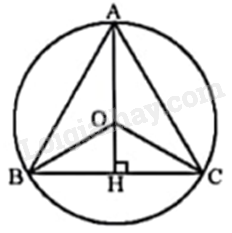
Vì tam giác ABC đều nội tiếp đường tròn (O) nên O là trọng tâm, trực tâm của tam giác ABC.
Gọi H là giao điểm của AO và BC nên AH là trung trực đồng thời là đường cao trong tam giác đều ABC.
Do đó: \(OA = \frac{{BC\sqrt 3 }}{3} \Rightarrow BC = \sqrt 3 OA = 2\sqrt 3 \left( {cm} \right)\).
Vậy cạnh của tam giác đều bằng \(2\sqrt 3 cm\).