Giải bài tập 9.28 trang 89 SGK Toán 9 tập 2 - Kết nối tri thức
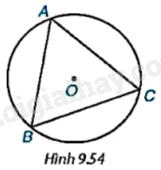
Cho tam giác đều ABC nội tiếp đường tròn (O) như Hình 9.54. Phép quay ngược chiều ({60^o}) tâm O biến các điểm A, B, C lần lượt thành các điểm D, E, F. Chứng minh rằng ADBECF là một lục giác đều.
Đề bài
Cho tam giác đều ABC nội tiếp đường tròn (O) như Hình 9.54. Phép quay ngược chiều \({60^o}\) tâm O biến các điểm A, B, C lần lượt thành các điểm D, E, F. Chứng minh rằng ADBECF là một lục giác đều.
Phương pháp giải - Xem chi tiết
Chứng minh \(AD = BD = BE = EC = FC = FA\) và \(\widehat {DAF} = \widehat {AFC} = \widehat {FCE} = \widehat {CEB} = \widehat {EBD} = \widehat {BDA} = {120^o}\), suy ra ADBECF là lục giác đều.
Lời giải chi tiết
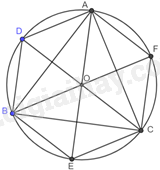
Vì lục giác ADBECF nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE = OF\).
Vì phép quay ngược chiều \({60^o}\) tâm O biến các điểm A, B, C lần lượt thành các điểm D, E, F nên \(\widehat {AOD} = \widehat {BOE} = \widehat {COF} = {60^o}\).
Vì tam giác ABC đều nên AO, BO là các đường phân giác của tam giác ABC.
Ta có: \(\widehat {BAO} = \widehat {ABO} = \frac{1}{2}\widehat {ABC} = {30^o}\)
Tam giác OAB có: \(\widehat {BOA} = {180^o} - \widehat {BAO} - \widehat {ABO} = {120^0}\).
Suy ra: \(\widehat {BOD} = \widehat {AOB} - \widehat {AOD} = {60^o}\)
Tam giác AOD cân tại O (do \(OA = OD\)), mà \(\widehat {AOD} = {60^o}\) nên tam giác DAO đều.
Do đó, \(DA = AO = OD,\widehat {DAO} = \widehat {ADO} = {60^o}\)
Tương tự ta có: \(DO = OB = BD,\widehat {ODB} = \widehat {OBD} = {60^o}\), \(EO = OB = BE,\widehat {OEB} = \widehat {OBE} = {60^o}\), \(EO = OC = CE,\widehat {OEC} = \widehat {OCE} = {60^o}\), \(FO = OC = CF,\widehat {OFC} = \widehat {OCF} = {60^o}\), \(FO = OA = AF,\widehat {OFA} = \widehat {OAF} = {60^o}\)
Do đó, \(AD = BD = BE = EC = FC = FA\) và \(\widehat {DAF} = \widehat {AFC} = \widehat {FCE} = \widehat {CEB} = \widehat {EBD} = \widehat {BDA} = {120^o}\)
Vậy ADBECF là lục giác đều.