Giải câu hỏi trắc nghiệm trang 72 vở thực hành Toán 9
Cho tam giác ABC có (widehat A = {90^o}) (H 4.2). A. (sin B = frac{{AB}}{{BC}}). B. (cos C = frac{{AC}}{{AB}}). C. (tan B = frac{{AC}}{{AB}}). D. (cot C = frac{{AB}}{{BC}}).
Chọn phương án đúng trong mỗi câu sau:
Câu 1
Trả lời Câu 1 trang 72 Vở thực hành Toán 9
Cho tam giác ABC có \(\widehat A = {90^o}\) (H 4.2).
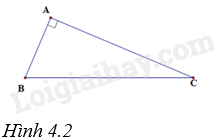
A. \(\sin B = \frac{{AB}}{{BC}}\).
B. \(\cos C = \frac{{AC}}{{AB}}\).
C. \(\tan B = \frac{{AC}}{{AB}}\).
D. \(\cot C = \frac{{AB}}{{BC}}\).
Phương pháp giải:
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có:
+ Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề gọi là tan của \(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối gọi là cot của \(\alpha \).
Lời giải chi tiết:
Vì tam giác ABC có \(\widehat A = {90^o}\) nên \(\tan B = \frac{{AC}}{{AB}}\)
Chọn C
Câu 2
Trả lời Câu 2 trang 72 Vở thực hành Toán 9
Cho tam giác ABC có \(\widehat A = {90^o}\) và \(\widehat C = {30^o}\) như trên Hình 4.3. Tìm khẳng định sai trong các khẳng định sau?
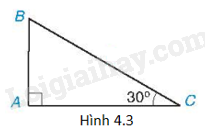
A. \(\sin B = \frac{{\sqrt 3 }}{2}\).
B. \(\cos C = \frac{{\sqrt 3 }}{2}\).
C. \(\tan B = \sqrt 3 \).
D. \(\cot B = \frac{1}{2}\).
Phương pháp giải:
+ Tính góc B.
+ Sử dụng bảng giá trị lượng giác của các góc 30 độ và 60 để tính.
Lời giải chi tiết:
Vì tam giác ABC có \(\widehat A = {90^o}\) nên \(\widehat B = {90^o} - \widehat C = {60^o}\).
Suy ra \(\sin B = \cos C = \sin {60^o} = \frac{{\sqrt 3 }}{2};\tan B = \tan {60^o} = \sqrt 3 ;\cot B = \cot {60^o} = \frac{{\sqrt 3 }}{3}\).
Chọn D
Câu 3
Trả lời Câu 3 trang 72 Vở thực hành Toán 9
Cho \(\alpha \), \(\beta \) là hai góc nhọn trong tam giác ABC (H.4.4). Khi đó
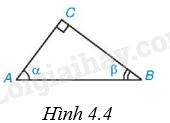
A. \(\sin \alpha = \tan \beta \).
B. \(\cos \alpha = \cot \beta \).
C. \(\tan \alpha = - \cot \beta \).
D. \(\cot \alpha = \tan \beta \).
Phương pháp giải:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Lời giải chi tiết:
Vì tam giác ABC vuông tại C nên \(\widehat A + \widehat B = {90^o}\), suy ra \(\alpha + \beta = {90^o}\). Do đó, \(\cot \alpha = \tan \beta \).
Chọn D
Câu 4
Trả lời Câu 4 trang 72 Vở thực hành Toán 9
A. \(\sin {82^o} = - \cos {8^o}\).
B. \(\cos {75^o} = \sin {16^o}\).
C. \(\cot {52^o} = - \tan {28^o}\).
D. \(\tan {30^o}40' = \cot {59^o}20'\).
Phương pháp giải:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Lời giải chi tiết:
Vì \({30^o}40' + {59^o}20' = {90^o}\) nên \(\tan {30^o}40' = \cot {59^o}20'\)
Chọn D