Giải khởi động trang 30 Chuyên đề học tập Toán 11 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Trong sách báo, tranh ảnh hay trong thực tế có những hình ảnh với hình dạng hoàn toàn giống nhau, chỉ khác nhau về kích thước. Những hình như vậy có liên quan gì về mặt hình học và phép biến hình nào đã tạo ra hình này từ hình kia?

Lời giải chi tiết

⦁ Những hình như vậy có cùng hình dạng nhưng khác kích thước.

⦁ Ta xét cụ thể một hình là hình hai con mèo:

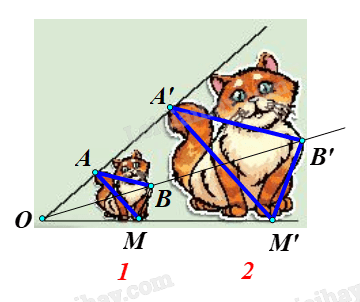
• Giả sử O là điểm cố định trên hình hai con mèo, M là một điểm trên hình con mèo 1 (như hình vẽ).

Lấy điểm M’ là điểm sao cho \(\overrightarrow {OM'}  = k\overrightarrow {OM} \) \(\left( {k{\rm{ }} > {\rm{ }}0} \right),\)khi đó điểm M’ có vị trí trên hình con mèo 2 tương ứng với điểm M trên hình con mèo 1.

Lấy điểm A’ sao cho \(\overrightarrow {OA'}  = k\overrightarrow {OA} \), với \(k{\rm{ }} > {\rm{ }}0,\) ta được điểm A’ có vị trí trên hình con mèo 2 tương ứng với điểm A trên hình con mèo 1.

Tương tự như vậy, với mỗi điểm B bất kì trên hình con mèo 1, ta lấy điểm B’ sao cho \(\overrightarrow {OB'}  = k\overrightarrow {OB} \,\left( {k{\rm{ }} > {\rm{ }}0} \right)\;\)  thì ta được tập hợp các điểm B’ tạo thành hình con mèo 2.

Vì vậy phép biến hình biến hình con mèo 1 thành hình con mèo 2 là phép biến hình biến mỗi điểm N bất kì thành điểm N’ sao cho \(\overrightarrow {ON'}  = k\overrightarrow {ON} \)

• Chứng minh tương tự với các hình ảnh khác, ta cũng được kết quả như trên.

Vậy phép biến hình cần tìm là phép biến hình biến mỗi điểm M bất kì trên hình kia thành điểm M’ trên hình này sao cho \(\overrightarrow {OM'}  = k\overrightarrow {OM} \),với O là điểm cố định và k là một số thực, \(k{\rm{ }} \ne {\rm{ }}0.\)