Giải mở đầu trang 41 Chuyên đề học tập Toán 11 - Kết nối tri thức — Không quảng cáo

Đề bài

Trong lí thuyết đồ thị, bài toán Bảy câu cầu ở Königsberg (nay là thành phố Kaliningrad, nước Nga) được phát biểu như sau: Thành phố có 7 cây cầu bắc qua sông như Hình 2.15a dưới đây, có thể nào đi dạo qua khắp các cây cầu nhưng mỗi cầu chỉ đi qua một lần không?

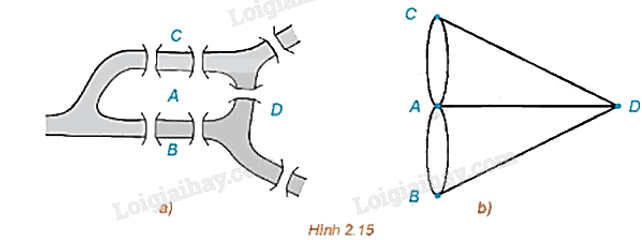
Nếu ta coi mỗi khu vực A, B, C, D của thành phố là một đỉnh, mỗi cầu qua lại hai khu vực như một cạnh nối hai đỉnh, thì bản đồ thành phố Königsberg là một đa đồ thị như Hình 2.15b. Vấn đề đặt ra chính là: Có thể vẽ được Hình 2.15b bằng một nét liền hay không?

Lời giải chi tiết

Sau bài học này, ta sẽ giải quyết được bài toán trên như sau:

Xét đa đồ thị G ở Hình 2.15b. Vì các đỉnh A, B, C, D đều có bậc lẻ nên theo Định lí 2, G không có đường đi Euler và không có cả chu trình Euler.

Vậy không thể nào đi dạo qua khắp các cây cầu của thành phố Königsberg mà mỗi cầu chỉ đi qua một lần.