Giải mục 1 trang 26, 27, 28, 29, 30 Chuyên đề học tập Toán 11 - Cánh diều — Không quảng cáo

Hoạt động 1

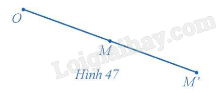
Trong mặt phẳng cho điểm O. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho $\overrightarrow {OM'}  = 2\overrightarrow {OM}$ ( Hình 47 ).

Phương pháp giải:

Quan sát hình 47, xác định M’ sao cho độ dài OM' = 2OM, và $\overrightarrow {OM} ;\,\overrightarrow {OM'}$ cùng hướng.

Lời giải chi tiết:

Cách xác định:

- Lấy điểm O và điểm M bất kì;

- Trên tia OM, lấy điểm M' sao cho OM' = 2OM.

Khi đó ta có $\overrightarrow {OM'}  = 2\overrightarrow {OM}$ (tham khảo Hình 47 ).

Luyện tập 1

Cho tam giác ABC có O là trung điểm của cạnh BC. Xác định ảnh của tam giác ABC trong phép vị tự tâm O tỉ số $k = \frac{1}{2}$ .

Phương pháp giải:

Tìm ảnh của A, B, C qua phép vị tự tâm O, tỉ số $k = \frac{1}{2}$ là A’B’C’. Khi đó ảnh của tam giác ABC qua phép vị tự chính là tam giác A’B’C’.

Lời giải chi tiết:

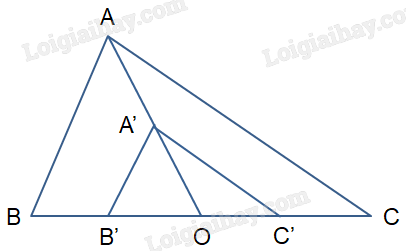
Gọi A', B', C' lần lượt là ảnh của A, B, C qua phép vị tự tâm O tỉ số $k = \frac{1}{2}$. Khi đó ta có:

$\overrightarrow {OA'}  = \frac{1}{2}\overrightarrow {OA} ;\,\,\overrightarrow {OB'}  = \frac{1}{2}\overrightarrow {OB} ;\,\,\overrightarrow {OC'}  = \frac{1}{2}\overrightarrow {OC}$. Do đó, các điểm A', B', C' lần lượt là trung điểm của OA, OB, OC.

Vậy ảnh của tam giác ABC trong phép vị tự tâm O tỉ số $k = \frac{1}{2}$ là tam giác A'B'C' với A', B', C' lần lượt là trung điểm của OA, OB, OC.

Hoạt động 2

Cho phép vị tự tâm O tỉ số k và hai điểm A, B. Giả sử $A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right).$

a) Biểu diễn các vectơ $\overrightarrow {OA'} ,\,\overrightarrow {OB'}$ lần lượt theo các vectơ $\overrightarrow {OA} ,\,\overrightarrow {OB}$ .

b) Biểu diễn các vectơ $\overrightarrow {A'B'}$ theo vectơ $\overrightarrow {AB}$ . Từ đó, tìm mối liên hệ độ dài giữa hai đoạn thẳng A'B' và AB.

Phương pháp giải:

Sử dụng quy tắc hiệu và tính chất $A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right) \Rightarrow \overrightarrow {OA'}  = k\overrightarrow {OA}$.

Lời giải chi tiết:

a) Vì $A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right)$ nên $\overrightarrow {OA'}  = k\overrightarrow {OA} ,\,\,\overrightarrow {OB'}  = k\overrightarrow {OB}$

b) Ta có: $\overrightarrow {A'B'}  = \overrightarrow {OB'}  - \overrightarrow {OA'}  = k\overrightarrow {OB}  - k\overrightarrow {OA}  = k\left( {\overrightarrow {OB}  - \overrightarrow {OA} } \right) = k\overrightarrow {AB}$ (theo quy tắc hiệu).

Vậy $\overrightarrow {A'B'}  = k\overrightarrow {AB}$, từ đó suy ra $A'B' = \left| k \right|AB.$

Hoạt động 3

Cho phép vị tự tâm O tỉ số k và ba điểm A, B, C thẳng hàng sao cho B nằm giữa A và C. Giả sử $A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right),{\rm{ }}C' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( C \right).$

a) Biểu diễn các vectơ $\overrightarrow {B'A'} ,\,\overrightarrow {B'C'}$ lần lượt theo các vectơ $\overrightarrow {BA} ,\,\overrightarrow {BC}$ .

b) Hai vectơ $\overrightarrow {BA}$ và $\overrightarrow {BC}$ có ngược hướng không?

c) Hai vectơ $\overrightarrow {B'A'}$ và $\overrightarrow {B'C'}$ có ngược hướng không? Từ đó, nêu mối quan hệ giữa ba điểm A', B', C'.

Phương pháp giải:

Làm tương tự Hoạt động 2, sử dụng quy tắc hiệu và tính chất $A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right) \Rightarrow \overrightarrow {OA'}  = k\overrightarrow {OA}$.

Lời giải chi tiết:

a) Vì $A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right),{\rm{ }}C' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( C \right).$ nên $\overrightarrow {B'A'}  = k\overrightarrow {BA}$  và $\overrightarrow {B'C'}  = k\overrightarrow {BC}$.

b) Vì A, B, C thẳng hàng và B nằm giữa A và C nên hai vectơ $\overrightarrow {BA}$ và $\overrightarrow {BC}$ngược hướng với nhau.

c) +) Với k > 0, ta có:

$\overrightarrow {B'A'}  = k\overrightarrow {BA}$ nên hai vectơ $\overrightarrow {B'A'} ,\,\overrightarrow {BA}$ cùng hướng với nhau.

$\overrightarrow {B'C'}  = k\overrightarrow {BC}$ nên hai vectơ $\overrightarrow {B'C'} ,\,\overrightarrow {BC}$ cùng hướng với nhau.

Mà hai vectơ $\overrightarrow {BA}$ và $\overrightarrow {BC}$ ngược hướng với nhau nên hai vectơ $\overrightarrow {B'A'}$  và $\overrightarrow {B'C'}$ ngược hướng với nhau.

+) Với k < 0, ta có:

$\overrightarrow {B'A'}  = k\overrightarrow {BA}$ nên hai vectơ $\overrightarrow {B'A'}$ và  $\overrightarrow {BA}$  ngược hướng với nhau.

$\overrightarrow {B'C'}  = k\overrightarrow {BC}$ nên hai vectơ $\overrightarrow {B'C'}$ và $\overrightarrow {BC}$ ngược hướng với nhau.

Mà hai vectơ $\overrightarrow {BA}$ và $\overrightarrow {BC}$ ngược hướng với nhau nên hai vectơ  và  ngược hướng với nhau.

Từ đó suy ra với k ≠ 0 thì hai vectơ null  và $\overrightarrow {B'C'}$ ngược hướng với nhau.

Do đó, ba điểm A', B', C' thẳng hàng và B' nằm giữa hai điểm A' và C'.

Luyện tập 2

Cho đường tròn (C) có tâm O bán kính R. Xác định ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số $k =  - \frac{1}{2}$.

Phương pháp giải:

Tìm ảnh của tâm O qua phép vị tự và $R' = \;\left| k \right|R$

Lời giải chi tiết:

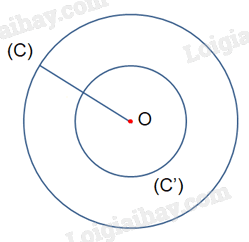
Qua phép vị tự tâm O tỉ số $k =  - \frac{1}{2}$ thì điểm O biến thành chính nó. Do đó, ảnh của đường tròn (C) là đường tròn (C') có tâm O và bán kính $R' = \;\left| { - \frac{1}{2}} \right|R = \frac{1}{2}R$.