Giải mục 2 trang 6, 7, 8, 9 Chuyên đề học tập Toán 11 - Cánh diều
Cho vectơ (vec u) và điểm M trong mặt phẳng.
Hoạt động 2
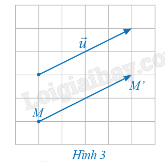
Cho vectơ \(\vec u\) và điểm M trong mặt phẳng. Hãy xác định điểm M' trong mặt phẳng sao cho \(\overrightarrow {MM'} = \vec u\) ( Hình 3 ).
Phương pháp giải:
Quan sát hình 3, xác định điểm M' thỏa mãn \(\overrightarrow {MM'} = \vec u\)
Lời giải chi tiết:
Cách xác định điểm M' trong mặt phẳng sao cho: \(\overrightarrow {MM'} = \vec u\)
- Qua M kẻ đường thẳng d song song với giá của vectơ (hoặc trùng với giá của vectơ \(\vec u\) nếu điểm M thuộc giá của vectơ \(\vec u\)).
- Trên đường thẳng d, lấy điểm M' sao cho \(MM' = \left( {\vec u} \right)\), và hướng từ M đến M' cùng hướng với vectơ \(\vec u\). (Tham khảo Hình 3 )
Luyện tập 1
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm N, P, C, A, M qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} .\)
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
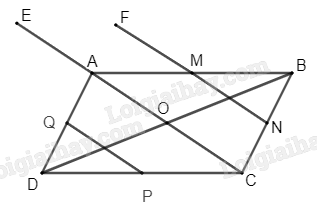
+ Vì M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC, suy ra MN // AC và MN = AC. Do đó, \(\overrightarrow {NM} = \frac{1}{2}\overrightarrow {CA} \,\,(1)\).Vì O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD nên O là trung điểm của AC, do đó \(OA = \frac{1}{2}AC\). Suy ra \(\overrightarrow {OA} = \frac{1}{2}\overrightarrow {CA} \) (2).
Từ (1) và (2) suy ra \(\overrightarrow {NM} = \overrightarrow {OA} \,\,(3)\)
Vậy ảnh của điểm N qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) là điểm M.
+ Vì P và Q lần lượt là trung điểm của CD và DA nên PQ là đường trung bình của tam giác ADC, suy ra PQ // AC và \(PQ = \frac{1}{2}AC\). Do đó, \(\overrightarrow {PQ} = \frac{1}{2}\overrightarrow {CA} \) (4)
Từ (2) và (4) suy ra \(\overrightarrow {PQ} = \overrightarrow {OA} \)
Vậy ảnh của điểm P qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) là điểm Q.
+ Vì O là trung điểm của AC nên \(\overrightarrow {CO} = \overrightarrow {OA} \).
Vậy ảnh của điểm C qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) là điểm O.
+ Lấy điểm E đối xứng với điểm O qua điểm A, khi đó A là trung điểm của OE.
Suy ra \(\overrightarrow {AE} = \overrightarrow {OA} \).
Vậy ảnh của điểm A qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) là điểm E.
+ Lấy điểm F đối xứng với điểm N qua điểm M, khi đó M là trung điểm của NF.
Suy ra \(\overrightarrow {NM} = \overrightarrow {MF} \,\,(5)\)
Từ (3) và (5) suy ra \(\overrightarrow {MF} = \overrightarrow {OA} \).
Vậy ảnh của điểm M qua phép tịnh tiến theo vectơ \(\overrightarrow {OA} \)
Hoạt động 3
Cho phép tịnh tiến \({T_{\vec u}}\) và hai điểm M, N. Giả sử \(M' = {T_{\vec u}}\left( M \right),\,N' = {T_{\vec u}}\left( N \right)\)
a) Biểu diễn các vectơ \(\overrightarrow {MM'} \,\) và \(\overrightarrow {NN'} \) theo \(\vec u\).
b) Tìm mối liên hệ giữa hai vectơ \(\overrightarrow {M'N'} \) và \(\overrightarrow {MN} \).
c) So sánh các đoạn thẳng M'N' và MN.
Phương pháp giải:
+ Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
+ Dựa vào quy tắc 3 điểm để làm
Lời giải chi tiết:
a) Vì \(M' = {T_{\vec u}}\left( M \right)\) nên \(\overrightarrow {MM'} = \vec u\).
Vì \(N' = {T_{\vec u}}\left( N \right)\) nên \(\overrightarrow {NN'} = \vec u\).
b) Theo quy tắc ba điểm ta có:
\(\overrightarrow {MN} = \overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow {MM'} + \overrightarrow {M'N'} + \overrightarrow {N'N} = \vec u + \overrightarrow {M'N'} + \left( { - \overrightarrow {NN'} } \right) = \vec u + \overrightarrow {M'N'} + \left( { - \vec u} \right) = \overrightarrow {M'N'} \)Vậy \(\overrightarrow {MN} = \overrightarrow {M'N'} \).
c) Vì \(\overrightarrow {MN} = \overrightarrow {M'N'} \) nên MN = M'N'.
Hoạt động 4
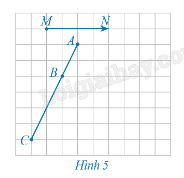
Xét phép tịnh tiến theo vectơ \(\overrightarrow {MN} \) ( Hình 5 ).
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép tịnh tiến trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
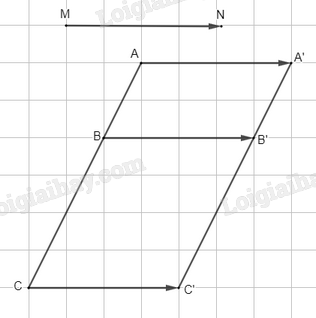
a) Vì A', B', C' lần lượt là ảnh của các điểm A, B, C qua phép tịnh tiến theo vectơ \(\overrightarrow {MN} \) nên ta xác định các điểm A', B', C' bằng cách lấy các điểm đó thỏa mãn: \(\overrightarrow {AA'} = \overrightarrow {MN} ,\,\overrightarrow {BB'} = \overrightarrow {MN} ,\,\overrightarrow {CC'} = \overrightarrow {MN} \) (như hình vẽ trên).
b) Vì \(\overrightarrow {AA'} = \overrightarrow {MN} ,\,\overrightarrow {BB'} = \overrightarrow {MN} \) nên \(\overrightarrow {AA'} = \overrightarrow {BB'} \), suy ra ABB'A' là hình bình hành.
Do đó, \(\overrightarrow {AB} = \overrightarrow {A'B'} \,\,(1)\)
Vì \(\overrightarrow {AA'} = \overrightarrow {MN} ,\,\overrightarrow {CC'} = \overrightarrow {MN} \) nên \(\overrightarrow {AA'} = \overrightarrow {CC'} \), suy ra ACC'A' là hình bình hành.
Do đó, \(\overrightarrow {AC} = \overrightarrow {A'C'} \,\,(2)\)
Vì A, B, C là 3 điểm thẳng hàng với B nằm giữa A và C nên \(\overrightarrow {AB} = k\overrightarrow {AC} \,\,(k \ne 0)\) (3).
Từ (1), (2) và (3) suy ra \(\overrightarrow {A'B'} = k\overrightarrow {A'C'} \)
Vậy ba điểm A', B', C' thẳng hàng với B' nằm giữa A' và C'.
Luyện tập 2
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm O(0; 0) và bán kính R = 3. Xác định ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ \(\vec u = \left( {3;\,4} \right)\)
Phương pháp giải:
Xác định ảnh của tâm O qua phép tịnh tiến bằng cách:
Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Sau đó xác định ảnh của đường tròn qua phép tịnh tiến.
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ \(\vec u = \left( {3;\,4} \right)\) là một đường tròn bán kính bằng 3, gọi là (C').
Gọi O' là tâm của (C'). Ta có O' là ảnh của O qua phép tịnh tiến theo vectơ \(\vec u = \left( {3;\,4} \right)\) nên \(\overrightarrow {OO'} = \vec u = \left( {3;\,4} \right)\). Suy ra O'(3; 4).
Vậy ảnh của đường tròn (C) là đường tròn (C') có tâm O'(3; 4), bán kính bằng 3.