Giải mục 1 trang 54,55,56 SGK Toán 12 tập 2 - Kết nối tri thức
PHƯƠNG TRÌNH MẶT CẦU
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 54 SGK Toán 12 Kết nối tri thức
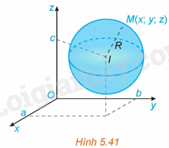
Trong không gian Oxyz, cho mặt cầu (S) tâm và bán kính R (H.5.41). Khi đó, một điểm thuộc mặt cầu (S) khi và chỉ khi nó thỏa mãn điều kiện gì?
Phương pháp giải:
Sử dụng kiến thức về mặt cầu tâm để tìm điều kiện:
+ Mặt cầu tâm I bán kính R là tập hợp các điểm trong không gian cách I một khoảng bằng R.
+ Mỗi đường thẳng đi qua tâm mặt cầu đều cắt mặt cầu tại hai điểm phân biệt, đoạn thẳng nối hai điểm đó được gọi là đường kính mặt cầu. Mỗi đường kính của mặt cầu đều có trung điểm là tâm mặt cầu và có độ dài bằng hai lần bán kính mặt cầu.
Lời giải chi tiết:
Mặt cầu tâm I bán kính R là tập hợp các điểm trong không gian cách I một khoảng bằng R.
Do đó, điểm thuộc mặt cầu (S) khi và chỉ khi .
LT1
Trả lời câu hỏi Luyện tập 1 trang 55 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) có phương trình \({\left( {x + 2} \right)^2} + {y^2} + {\left( {z + \frac{1}{2}} \right)^2} = \frac{9}{4}\).
a) Xác định tâm và bán kính của (S).
b) Hỏi điểm \(M\left( {2;0;1} \right)\) nằm trong, nằm ngoài hay thuộc mặt cầu (S)?
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để xác định tâm và bán kính của mặt cầu: Trong không gian Oxyz, mặt cầu (S) tâm \(I\left( {a;{\rm{ }}b;{\rm{ }}c} \right)\), bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Sử dụng kiến thức về phương trình mặt cầu để xác định vị trí của điểm so với mặt cầu: Cho mặt cầu (S) tâm I, bán kính R và điểm M bất kì trong không gian:
+ Nếu \(IM = R\) thì M nằm trên mặt cầu (S) tâm I.
+ Nếu \(IM > R\) thì M nằm ngoài mặt cầu (S) tâm I.
+ Nếu \(IM < R\) thì M nằm trong mặt cầu (S) tâm I.
Lời giải chi tiết:
a) Ta viết lại phương trình mặt cầu (S) dưới dạng:
\({\left[ {x - \left( { - 2} \right)} \right]^2} + {\left( {y - 0} \right)^2} + {\left[ {z - \left( { - \frac{1}{2}} \right)} \right]^2} = {\left( {\frac{3}{2}} \right)^2}\)
Do đó, mặt cầu (S) có tâm \(I\left( { - 2;0;\frac{{ - 1}}{2}} \right)\) và bán kính \(R = \frac{3}{2}\).
b) Ta có: \(MI = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {0 - 0} \right)}^2} + {{\left( {\frac{{ - 1}}{2} - 1} \right)}^2}} = \frac{{\sqrt {73} }}{2} > \frac{3}{2} = R\) nên điểm \(M\left( {2;0;1} \right)\) nằm ngoài mặt cầu (S).
LT2
Trả lời câu hỏi Luyện tập 2 trang 55 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, viết phương trình mặt cầu (S) trong các trường hợp sau:
a) Tâm là gốc tọa độ, bán kính \(R = 1\).
b) Đường kính AB, với \(A\left( {1; - 1;2} \right),B\left( {2; - 3; - 1} \right)\).
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để viết phương trình mặt cầu: Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c), bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Lời giải chi tiết:
a) Mặt cầu (S) có tâm \(O\left( {0;0;0} \right)\), bán kính \(R = 1\) nên có phương trình là: \({x^2} + {y^2} + {z^2} = 1\)
b) Đoạn thẳng AB có trung điểm là \(E\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)\).
Mặt cầu (S) có bán kính \(R = \frac{1}{2}AB = \frac{1}{2}\sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( { - 3 + 1} \right)}^2} + {{\left( { - 1 - 2} \right)}^2}} = \frac{{\sqrt {14} }}{2}\) và tâm \(E\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)\). Do đó, (S): \({\left( {x - \frac{3}{2}} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - \frac{1}{2}} \right)^2} = \frac{7}{2}\)
LT3
Trả lời câu hỏi Luyện tập 3 trang 56 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho (S) là tập hợp các điểm \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) có tọa độ thỏa mãn phương trình: \({x^2} + {y^2} + {z^2} - 4x + 6y - 12 = 0\). Chứng minh rằng (S) là một mặt cầu. Xác định tâm và bán kính của mặt cầu đó.
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để chứng minh: Trong không gian Oxyz, mặt cầu (S) tâm \(I\left( {a;b;c} \right),\) bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
Lời giải chi tiết:
Ta có: \({x^2} + {y^2} + {z^2} - 4x + 6y - 12 = 0\)
\( \Leftrightarrow \left( {{x^2} - 4x + 4} \right) + \left( {{y^2} + 6y + 9} \right) + {z^2} = 25\)\( \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} + {z^2} = {5^2}\)
Do đó, (S) là mặt cầu có tâm \(I\left( {2; - 3;0} \right)\) và bán kính \(R = 5\).
LT4
Trả lời câu hỏi Luyện tập 4 trang 56 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho mặt cầu (S) có phương trình:
\({x^2} + {y^2} + {z^2} + 4x - 5y + 6z + \frac{{25}}{4} = 0\).
Xác định tâm, tính bán kính của (S).
Phương pháp giải:
Sử dụng kiến thức về phương trình mặt cầu để tính: Với a, b, c, d là các hằng số, phương trình \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có thể viết lại thành \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {a^2} + {b^2} + {c^2} - d\) và là phương trình của một mặt cầu (S) khi và chỉ khi \({a^2} + {b^2} + {c^2} - d > 0\). Khi đó, (S) có tâm \(I\left( {a;{\rm{ }}b;{\rm{ }}c} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Lời giải chi tiết:
Phương trình mặt cầu (S) đã cho tương ứng với \(a = - 2;b = \frac{5}{2};c = - 3,d = \frac{{25}}{4}\)
Nên mặt cầu (S) có tâm \(I\left( { - 2;\frac{5}{2}; - 3} \right)\), bán kính \(R = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {\frac{5}{2}} \right)}^2} + {{\left( { - 3} \right)}^2} - \frac{{25}}{4}} = \sqrt {13} \)