Giải mục 1 trang 65, 66, 67 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm của đường trung trực của đoạn thẳng AB và BC (Hình 1). a) So sánh độ dài của đoạn thẳng OA, OB và OC. b) Vẽ đường tròn đi qua ba điểm A, B, C.
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 65 SGK Toán 9 Chân trời sáng tạo
Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm của đường trung trực của đoạn thẳng AB và BC (Hình 1).
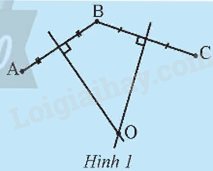
a) So sánh độ dài của đoạn thẳng OA, OB và OC.
b) Vẽ đường tròn đi qua ba điểm A, B, C.
Phương pháp giải:
Dựa vào tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Lời giải chi tiết:
a) Vì O thuộc đường trung trực của AB.
Suy ra OA = OB (tính chất đường trung trực) (1).
Vì O thuộc đường trung trực của BC.
Suy ra OC = OB (tính chất đường trung trực) (2).
Từ (1) và (2) suy ra OA = OB = OC
b)
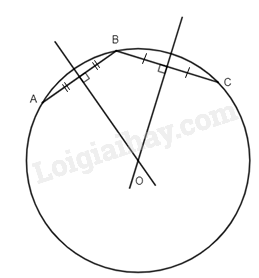
TH1
Trả lời câu hỏi Thực hành 1 trang 67 SGK Toán 9 Chân trời sáng tạo
Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm của đường trung Xác định tâm và bán kính của đường tròn ngoại tiếp mỗi tam giác sau:
a) Tam giác đều MNP có cạnh bằng 4;
b) Tam giác EFG có EF = 5 cm; EG = 3 cm; FG = 4cm.
Phương pháp giải:
- Dựa vào dữ kiện đề bài để vẽ hình.
- Dựa vào đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác và bán kính bằng \(\frac{{a\sqrt 3 }}{3}\).
- Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm cạnh huyền và bán kính bằng nửa cạnh huyền.
Lời giải chi tiết:
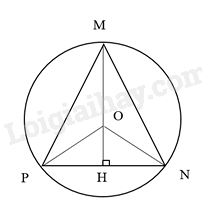
a) Vẽ đường cao MH của giác MNP, gọi O là điểm nằm trên MH sao cho
OM = \(\frac{2}{3}\) MH.
Do tam giác MNP đều nên O vừa là trọng tâm vừa là giao điểm của ba đường trung trực.
Bán kính đường tròn ngoại tiếp tam giác MNP là:
R = OH = \(\frac{{a\sqrt 3 }}{3} = \frac{{4\sqrt 3 }}{3}\) (cm).
b)
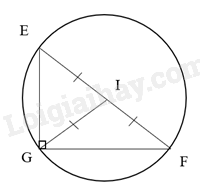
Ta có: \({5^2} = {3^2} + {4^2}\) nên \(E{F^2} = E{G^2} + F{G^2}\)
Suy ra tam giác EFG vuông tại G.
Gọi I là trung điểm của cạnh huyền EF. Ta có GI là đường trung tuyến ứng với cạnh huyền của tam giác EFG vuông tại G,
suy ra IG = IE = IF = \(\frac{{EF}}{2}\) = 2,5 cm
Vậy đường tròn tâm I bán kính 5 cm ngoại tiếp tam giác EFG.
VD1
Trả lời câu hỏi Vận dụng 1 trang 67 SGK Toán 9 Chân trời sáng tạo
Có ba tổ dựng lều ở ba vị trí A, B, C như Hình 6. Ban tổ chức đặt ba thùng có dung tích bằng nhau tại một điểm tập kết chung. Mỗi tổ có sáu người, được phát một chiếc gàu giống nhau, các thành viên trong tổ chia thành từng cặp cõng nhau, múc nước từ tại của mình về đổ vào thùng tại điểm tập kết. Thùng của tổ nào đầy trước thì tổ đó chiến thắng. Để trò chơi công bằng, cần tìm điểm tập kết cách đều ba lều. Hãy xác định điểm đó.
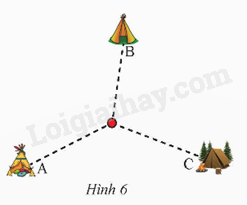
Phương pháp giải:
Dựa vào đường tròn ngoại tiếp có tâm là giao điểm của ba đường trung trực của tam giác và có bán kính bằng khoảng cách từ giao điểm đó đến một đỉnh bất kì của tam giác.
Lời giải chi tiết:
Điểm tập kết cách đều 3 lều tức khoảng cách từ điểm tập kết đều mỗi lều là như nhau tam giác. Điểm tập kết O là tâm đường tròn ngoại tiếp tam giác ABC.
Suy ra điểm tập kết O là giao điểm của ba đường trung trực của tam giác ABC. Khi vẽ, ta chỉ cần vẽ hai đường trung trực của tam giác ABC là ta có thể xác định được điểm O.