Giải mục 1 trang 74 SGK Toán 10 tập 1 - Kết nối tri thức
Ngày 8-12-2020, Trung Quốc và Nepal ra thông cáo chung khẳng định chiều cao mới đo được của đỉnh núi cao nhất thế giới Everest là 8 848,86 m. Trang và Hoà thực hiện đo thể tích một cốc nước bằng hai ống đồng có vạch chia được kết quả như Hình 5.1. Hãy lấy một ví dụ về số gần đúng. Gọi P là chu vi của đường tròn bán kính 1cm. Hãy tìm một giá trị gần đúng của P.
HĐ1
Ngày 8-12-2020, Trung Quốc và Nepal ra thông cáo chung khẳng định chiều cao mới đo được của đỉnh núi cao nhất thế giới Everest là 8 848,86 m.
(Theo Tuoitre.vn)
Trong các số được đưa ra ở tình huống mở đầu, số nào gần nhất với số được công bố ở trên?
Phương pháp giải:
Lấy 8 848,86 trừ đi các số xuất hiện ở tình huống mở đầu và so sánh các giá trị tuyệt đối của các hiệu vừa tìm được.
Lời giải chi tiết:
Ta có: \(\left| {8848,86 - 8848} \right| = 0,86\)
\(\left| {8848,86 - 8848,13} \right| = 0,73\)
\(\left| {8848,86 - 8844,43} \right| = 4,43\)
\(\left| {8848,86 - 8850} \right| = 1,14\)
Trong các số 0,86; 0,73; 4,43; 1,14 thì số 0,73 là số nhỏ nhất.
Do đó trong các số 8 848 m; 8 848,13 m; 8 844,43 m; 8 850 m thì số ; 8 848,13 m là số gần nhất với số được công bố ngày 8-12-2020.
Chú ý
Giá trị tuyệt đối |a-b| càng nhỏ thì a và b càng gần nhau.
HĐ2
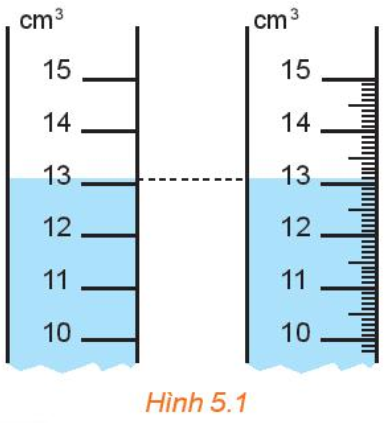
Trang và Hoà thực hiện đo thể tích một cốc nước bằng hai ống đồng có vạch chia được kết quả như Hình 5.1.
Hãy cho biết số đo thể tích trên mỗi ống.
Phương pháp giải:
Đọc các số xuất hiện tại vạch nước ở mỗi ống.
Lời giải chi tiết:
Giả sử ống nước thứ nhất là trang đo và ống nước thứ hai là Hòa đo.
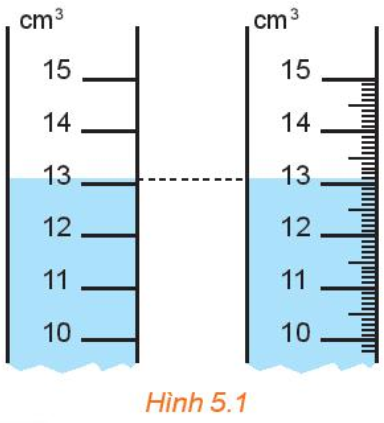
Khi đó ống thứ nhất đo được là 13\(c{m^3}\), ống thứ hai là 13,1\(c{m^3}\)
Chú ý
Với ống thứ hai thì có vạch chia nhỏ hơn.
Câu hỏi
Hãy lấy một ví dụ về số gần đúng.
Phương pháp giải:
Số gần đúng là số mà ta khó có thể biết được giá trị chính xác của nó mà chỉ tìm được giá trị xấp xỉ của nó mà thôi.
Lời giải chi tiết:
Ta không thể biết chính xác giá trị của \(\sqrt 3 \).
Số gần đúng của \(\sqrt 3 \) là 1,73.
Chú ý
Ta có thể lấy các số khác như \(\sqrt 2 ;\sqrt p \) với p là số nguyên tố hoặc số \(\pi \).
Luyện tập 1
Gọi P là chu vi của đường tròn bán kính 1cm. Hãy tìm một giá trị gần đúng của P.
Phương pháp giải:
Sử dụng công thức tính chu vi đường tròn \(P = 2\pi R\) với R là bán kính của đường tròn đó.
Cách bấm máy tính tìm \(\pi \):

Lời giải chi tiết:
Chu vi đường tròn là:
\(P = 2\pi R = 2\pi .1 = 2\pi \left( {cm} \right)\)
Bấm máy tính ta thấy \(2\pi \approx 6,28\)
Vậy \(P \approx 6,28cm\).
Chú ý
Ta có thể lấy số gần đúng khác của \(2\pi \) như: 6,283 hoặc 6,283185