Giải mục 1 trang 76, 77 SGK Toán 11 tập 2 - Kết nối tri thức
Có hai hộp đựng các quả bóng có cùng kích thước và khối lượng. Hộp I có 6 quả màu trắng và 4 quả màu đen.
HĐ 1
Có hai hộp đựng các quả bóng có cùng kích thước và khối lượng. Hộp I có 6 quả màu trắng và 4 quả màu đen. Hộp II có 1 quả màu trắng và 7 quả màu đen. Bạn Long lấy ngẫu nhiên một quả bóng từ hộp I, bạn Hải lấy ngẫu nhiên một quả bóng từ hộp II. Xét các biến cố sau:
A: “Bạn Long lấy được quả bóng màu trắng”;
B: “Bạn Hải lấy được quả bóng màu đen”.
a) Tính P(A), P(B) và P(AB).
b) So sánh P(AB) và P(A).P(B).
Phương pháp giải:
- \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\)
- Cho A và B là hai biến cố. Biến cố: “Cả A và B đều xảy ra” được gọi là biến cố giao của A và B, kí hiệu AB
Lời giải chi tiết:
a) \(P\left( A \right) = \frac{6}{{10}} = \frac{3}{5};P\left( B \right) = \frac{7}{8}\)
Không gian mẫu là tập hợp số cách Bạn Long lấy được một quả bóng từ hộp I và Bạn Hải lấy một quả bóng từ hộp II do đó \(n\left( \Omega \right) = 10.8 = 80\)
C: “Bạn Long lấy được quả màu trắng và bạn Hải lấy được quả màu đen”
Công đoạn 1: Bạn Long lấy được quả màu trắng có 6 cách
Công đoạn 2. Bạn Hải lấy được quả màu đen có 7 cách
Theo quy tắc nhân, tập hợp C có 6.7 = 42 (phần tử)
\(P\left( C \right) = P\left( {AB} \right) = \frac{{n\left( C \right)}}{{n\left( \Omega \right)}} = \frac{{42}}{{80}} = \frac{{21}}{{40}}\)
b) \(P\left( A \right).P\left( B \right) = \frac{3}{5}.\frac{7}{8} = \frac{{21}}{{40}}\)
Vậy P(AB) = P(A).P(B).
CH 1
Hai biến cố A và B trong HĐ1 độc lập hay không độc lập? Tại sao?
Phương pháp giải:
Cặp biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biển cố kia.
Lời giải chi tiết:
Nếu A xảy ra, tức là bạn Long lấy được quả bóng màu trắng từ hộp I. Vì bạn Hải lấy bóng từ hộp II vậy \(P\left( B \right) = \frac{7}{8}\)
Nếu A không xảy ra, tức là bạn Long lấy được quả bóng màu đen từ hộp I. Vì ban Hải lấy bóng từ hộp II vậy \(P\left( B \right) = \frac{7}{8}\)
Như vậy, xác suất xảy ra của biến cố B không thay đổi bởi việc xảy ra hay không xảy ra của biến cố A.
Vì hai bạn lấy từ 2 hộp khác nhau nên \(P\left( A \right) = \frac{3}{5}\) dù biến cố B xảy ra hay không xảy ra
Vậy A và B độc lập.
LT 1
Các học sinh lớp 11D làm thí nghiệm gieo hai loại hạt giống A và B. Xác suất để hai loại hạt giống A và B nảy mầm tương ứng là 0,92 và 0,88. Giả sử việc nảy mầm của hạt A và hạt B là độc lập với nhau. Dùng sơ đồ hình cây, tính xác suất để:
a) Hạt giống A nảy mầm còn hạt giống B không nảy mầm;
b) Hạt giống A không nảy mầm còn hạt giống B nảy mầm;
c) Ít nhất có một trong hai loại hạt giống nảy mầm.
Phương pháp giải:
Nếu hai biến cố A và B độc lập với nhau thì P(AB) = P(A).P(B).
Lời giải chi tiết:
Ta dùng sơ đồ hình cây để mô tả như sau:
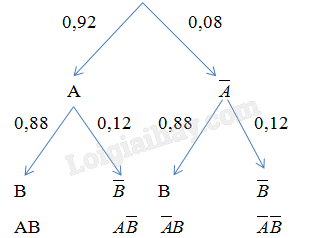
Theo sơ đồ hình cây, ta có:
a) \(P\left( {A\overline B } \right) = 0,92.0,12 = 0,1104\)
b) \(P\left( {\overline A B} \right) = 0,08.0,88 = 0,0704\)
c) \(P\left( {\overline A \overline B } \right) = 0,08.0,12 = 0,0096\)
\(P\left( {A \cup B} \right) = 1 - P\left( {\overline A \overline B } \right) = 1 - 0,0096 = 0,9904\)