Giải mục 1 trang 90, 91 SGK Toán 9 tập 1 - Chân trời sáng tạo — Không quảng cáo

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 90 SGK Toán 9 Chân trời sáng tạo

Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của $\widehat {AOB}$

Phương pháp giải:

Nhìn hình và nhận xét.

Lời giải chi tiết:

Đỉnh của $\widehat {AOB}$ trùng với tâm O của đường tròn (O; R)

Cạnh của $\widehat {AOB}$ là OA và OB đều bằng bán kính R.

TH1

Trả lời câu hỏi Thực hành 1 trang 90 SGK Toán 9 Chân trời sáng tạo

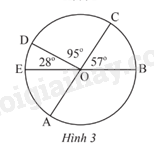
Tính số đo góc ở tâm $\widehat {EOA}$ và $\widehat {AOB}$ trong Hình 3. Biết AC và BE là hai đường kính của đường tròn (O).

Phương pháp giải:

Dựa vào tổng góc của đường tròn bằng 360 ^o .

Lời giải chi tiết:

Ta có AC là đường kính chia đường tròn tâm (O) thành hai phần bằng nhau, mỗi góc là 180 ^o .

Suy ra ta có $\widehat {EOA} = {180^o} - \widehat {COD} - \widehat {DOE} = {180^o} - {95^o} - {28^o} = {57^o}$

Tương tự , ta có: $\widehat {AOB} = {180^o} - \widehat {COB} = {180^o} - {57^o} = {123^o}$

VD1

Trả lời câu hỏi Vận dụng 1 trang 9 1 SGK Toán 9 Chân trời sáng tạo

Tính số đo góc ở tâm được tạo thành khi kim giờ quay:

a) Từ 7 giờ đến 9 giờ

b) Từ 9 giờ đến 12 giờ

Phương pháp giải:

Dựa vào đồng hồ như 1 đường tròn có 12 phần, tổng góc của đường tròn bằng 360 ^o .

Ta tính 1 giờ quay được bao nhiêu độ rồi tính 7 giờ đến 9 giờ và 9 giờ đến 12 giờ.

Lời giải chi tiết:

Ta có mỗi giờ thì kim giờ quay được $\frac{{{{360}^0}}}{{12}} = {30^o}$

a) Vậy từ 7 giờ đến 9 giờ, kim giờ quay được ${30^o}(9 - 7) = {60^o}$

b) Vậy từ 9 giờ đến 12 giờ, kim giờ quay được ${30^o}(12 - 9) = {90^o}$