Giải mục 2 trang 100, 101, 102 SGK Toán 8 tập 2 - Kết nối tri thức
Các tam giác vuông AHB và A'H'B' mô tả hai con dốc
HĐ1
Các tam giác vuông AHB và A'H'B' mô tả hai con dốc có chiều dài lần lượt là AB=13m, A′B′=6,5m và độ cao lần lượt là BH=5m, B′H′=2,5m. Độ dốc của hai con dốc lần lượt được tính bởi số đo các góc HAB và H'A'B'
- Nhận xét về hai đại lượng \(\frac{{A'H'}}{{AB}} = \frac{{B'H'}}{{BH}}\)
- Dùng định lí Pythagore để tính AH và A'H'
- So sánh các đại lượng \(\frac{{A'H'}}{{AH}} = \frac{{B'H'}}{{BH}}\)
- Hai tam giác vuông A'H'B' và AHB có đồng dạng không
Phương pháp giải:
- Tính các tỉ số theo yêu cầu của bài toán dựa vào độ dài đã biết.
Lời giải chi tiết:
- Có \(\frac{{A'H'}}{{AB}} = \frac{{B'H'}}{{BH}} = \frac{1}{2}\)
- Áp dụng định lý Pythagore có \(AH = 12 ;A'H' = 6 \)
- Có \(\frac{{A'H'}}{{AH}} = \frac{{B'H'}}{{BH}} = \frac{1}{2}\)
=> Hai tam giác vuông A'H'B' và AHB đồng dạng
CH2
Hãy chỉ ra các cặp tam giác vuông đồng dạng với nhau trong Hình 9.52, viết đúng kí hiệu đồng dạng.
Phương pháp giải:
Quan sát và sử dụng tỉ lệ của các cặp cạnh tương ứng để xác định.
Lời giải chi tiết:
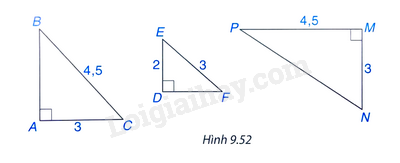
Tam giác ABC và tam giác DEF có:
\( \widehat A = \widehat D = 90^0 \)
\( \frac {AC}{DE} = \frac {BC}{EF} = \frac {3}{2} \)
\( \Rightarrow \Delta ABC \backsim \Delta DFE (ch - cgv) \)
LT2
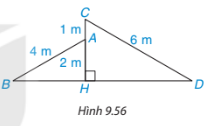
Một ngôi nhà với hai mái lệch AB, CD được thiết kế như Hình 9.56 sao cho CD = 6 m , AB = 4 m , HA = 2 m , AC = 1 m . Chứng tỏ \(\widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\) .
Phương pháp giải:
Chứng minh hai tam giác vuông HBA và tam giác HDC đòng dạng.
Lời giải chi tiết:
Xét hai tam giác vuông HBA và tam giác HDC nhận thấy:
\(\frac{{AB}}{{C{\rm{D}}}} = \frac{{AH}}{{CH}} = \frac{2}{3}\)
=> Hai tam giác đồng dạng
\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\)
VD
Bác Minh muốn thay chiếc ti vi có chiều ngang của màn hình là 72cm (loại 32 inch) bằng chiếc ti vi mới loại 55 inch có cùng tỉ lệ khung hình (tỉ lệ giữa hai kích thước màn hình). Hỏi nếu khoảng trống đặt ti vi là một hình vuông cạnh 1m thì có thể đặt chiếc tivi mới vào đó không? (Biết rằng 1 inch = 2,54m).
Phương pháp giải:
Gọi chiều ngang của chiếc ti vi mới là x.
Đổi các đơn vị inch sang cm
Tính chiều ngang của chiếc ti vi mới xem có vừa khoảng trống hình vuông 1m không?
Lời giải chi tiết:
- Gọi chiều ngang của chiếc ti vi mới là x
- Có 55 inch =139,7 cm
- Chiếc ti vi cũ có: chiều ngang màn hình là 72 cm
đường chéo của ti vi là: 32.2,54=81,28 (cm)
Có \(\frac{{81,28}}{{139,7}} = \frac{{72}}{x}\) => x=123,75cm=1,2375m
Vậy không thể đặt vừa chiếc ti vi vào khoảng trống hình vuông cạnh 1m