Giải mục 2 trang 67, 68, 69 SGK Toán 9 tập 2 - Chân trời sáng tạo
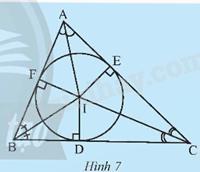
Gọi I là giao điểm ba đường phân giác của tam giác ABC. Vẽ ID, IE, IF lần lượt vuông góc với các cạnh BC, AC và AB (Hình 7). a) Chứng minh rằng IE = IF = ID. b) Vẽ đường tròn tâm I bán kính IE. Có nhận xét gì về vị trí của đường tròn này với ba cạnh của tam giác ABC?
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 67 SGK Toán 9 Chân trời sáng tạo
Gọi I là giao điểm ba đường phân giác của tam giác ABC. Vẽ ID, IE, IF lần lượt vuông góc với các cạnh BC, AC và AB (Hình 7).
a) Chứng minh rằng IE = IF = ID.
b) Vẽ đường tròn tâm I bán kính IE. Có nhận xét gì về vị trí của đường tròn này với ba cạnh của tam giác ABC?
Phương pháp giải:
- Xét \(\Delta \) FBI = \(\Delta \) DBI và \(\Delta \) IDC = \(\Delta \) IEC để suy ra IE = IF = ID.
- Nhìn hình và nhận xét.
Lời giải chi tiết:
a) Xét tam giác FBI vuông tại F và tam giác DBI vuông tại D có:
\(\widehat {FBI} = \widehat {IBD}\) (do BI là phân giác góc \(\widehat {FBD}\));
IB chung.
Suy ra \(\Delta \) FBI = \(\Delta \) DBI (cạnh huyền – góc nhọn).
Nên IF = ID (hai cạnh tương ứng) (1).
Xét \(\Delta \) IDC vuông tại D và \(\Delta \) IEC vuông tại E có:
\(\widehat {DCI} = \widehat {IEC}\) (do IC là phân giác góc \(\widehat {DEC}\));
IC chung.
Suy ra \(\Delta \) IDC = \(\Delta \) IEC (cạnh huyền – góc nhọn).
Nên ID = IE (hai cạnh tương ứng) (2).
Từ (1) và (2) suy ra IE = IF = ID.
b) Đường tròn này tiếp xúc với ba cạnh của tam giác tại các điểm F, D, E.
TH2
Trả lời câu hỏi Thực hành 2 trang 68 SGK Toán 9 Chân trời sáng tạo
Xác định tâm và bán kính đường tròn nội tiếp tam giác đều MNP có độ dài cạnh bằng 8 cm.
Phương pháp giải:
- Đọc kĩ dữ kiện đề bài để vẽ hình.
- Dựa vào: Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác và bán kính bằng \(\frac{{a\sqrt 3 }}{6}\).
Lời giải chi tiết:
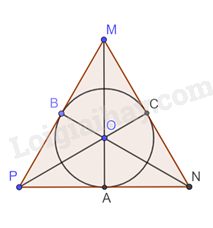
Gọi O là giao điểm của đường cao MA, NP và PC của tam giác MNP.
Ta có tam giác MNP đều nên MA, NB, PC là ba đường trung tuyến đồng thời là ba đường phân giác của tam giác.
Do đó, O là trọng tâm, đồng thời là tâm đường tròn nội tiếp tam giác MNP với bán kính r = OA = OB = OC.
Bán kính đường tròn ngoại tiếp tam giác là
r = \(\frac{{a\sqrt 3 }}{6} = \frac{{8\sqrt 3 }}{6} = \frac{{4\sqrt 3 }}{3}\) (cm).
VD2
Trả lời câu hỏi Vận dụng 2 trang 68 SGK Toán 9 Chân trời sáng tạo
Theo gợi ý trong Hình 10, nêu cách xác định hai điểm I và O của tình huống trong khởi động (trang 65).
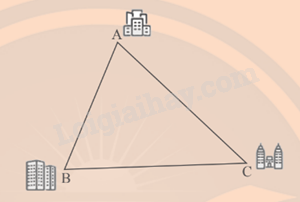
Ba cụm dân cư A, B, C nối với nhau bởi ba con đường AB, BC, CA như trong hình dưới đây. Người ta muốn tìm địa điểm O để xây một trường học và địa điểm I để lập một trạm cứu hộ xe, sao cho O cách đều ba điểm A, B, C và I cách đều ba con đường. Làm thế nào để xác định hai điểm O và I?
Phương pháp giải:
- Đọc kĩ dữ kiện đề bài để vẽ hình.
- Dựa vào đường tròn ngoại tiếp có tâm là giao điểm của ba đường trung trực của tam giác và có bán kính bằng khoảng cách từ giao điểm đó đến một đỉnh bất kì của tam giác.
- Dựa vào: Đường tròn nội tiếp tam giác có tâm là giao điểm của ba đường phân giác trong và bán kính bằng khoảng cách từ giao điểm đó đến một cạnh bất kì của tam giác.
Lời giải chi tiết:
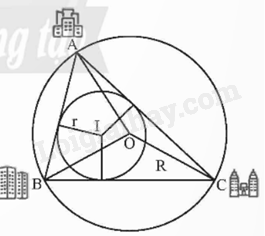
- Vẽ 3 đường trung trực của 3 đường thẳng AB, AC và BC, cho chúng cắt nhau từng đôi một. Điểm giao nhau đó là điểm O.
- Vẽ 3 đường phân giác trong của các góc \(\widehat A;\widehat B;\widehat C\) cho chúng cắt nhau từng đôi một và điểm giao nhau đó là điểm I.