Giải mục 2 trang 71 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho tứ giác ABCD nội tiếp đường tròn (O) (Hình 4). a) Chỉ ra các cung chắn bởi mỗi góc nội tiếp \(\widehat {DAB}\) và \(\widehat {DCB}\) b) Tính tổng số đo của các cung vừa tìm được. c) Nêu kết luận về tổng số đo của hai góc \(\widehat {DAB}\) và \(\widehat {DCB}\). d) Có nhận xét gì về tổng số đo của hai góc đối diện còn lại của tứ giác ABCD?
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 71 SGK Toán 9 Chân trời sáng tạo
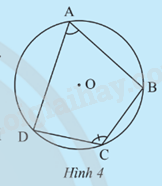
Cho tứ giác ABCD nội tiếp đường tròn (O) (Hình 4).
a) Chỉ ra các cung chắn bởi mỗi góc nội tiếp \(\widehat {DAB}\) và \(\widehat {DCB}\)
b) Tính tổng số đo của các cung vừa tìm được.
c) Nêu kết luận về tổng số đo của hai góc \(\widehat {DAB}\) và \(\widehat {DCB}\).
d) Có nhận xét gì về tổng số đo của hai góc đối diện còn lại của tứ giác ABCD?
Phương pháp giải:
- Dựa vào tính chất của số đo góc nội tiếp bằng \(\frac{1}{2}\) số đo cung bị chắn.
- Dựa vào tổng các góc của tứ giác bằng 360 o .
Lời giải chi tiết:
a) Góc \(\widehat {DAB}\) là góc nội tiếp chắn cung BD nhỏ.
Góc \(\widehat {DAB}\) là góc nội tiếp chắn cung BD lớn.
b) - Góc \(\widehat {DAB}\) là góc nội tiếp chắn cung BD nhỏ.
Suy ra \(\widehat {DAB} = \frac{1}{2}\) số đo cung BD nhỏ.
- Góc \(\widehat {DCB}\) là góc nội tiếp chắn cung BD lớn.
Suy ra \(\widehat {DCB} = \frac{1}{2}\) số đo cung BD lớn.
Ta có \(\widehat {DAB} + \widehat {DCB} = \frac{1}{2}\) (số đo cung BD nhỏ + số đo cung BD lớn)
= \(\frac{1}{2}\).360 o = 180 o .
c) Tổng số đo của hai góc \(\widehat {DAB}\) và \(\widehat {DCB}\) bằng 180 o .
d) Tổng số đo của hai góc đối diện còn lại của tứ giác ABCD là 180 o
(vì 360 o – 180 o = 180 o ).
TH2
Trả lời câu hỏi Thực hành 2 trang 71 SGK Toán 9 Chân trời sáng tạo
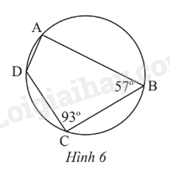
Tìm số đo các góc chưa biết của tứ giác ABCD trong Hình 6.
Phương pháp giải:
Dựa vào: Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180 o .
Lời giải chi tiết:
Tứ giác ABCD là tứ giác nội tiếp.
Do đó \(\widehat A + \widehat C = {180^o}\) suy ra \(\widehat A = {180^o} - \widehat C = {180^o} - {93^o} = {87^o}\).
\(\widehat B + \widehat D = {180^o}\) suy ra \(\widehat D = {180^o} - \widehat B = {180^o} - {57^o} = {123^o}\).
VD2
Trả lời câu hỏi Vận dụng 2 trang 71 SGK Toán 9 Chân trời sáng tạo
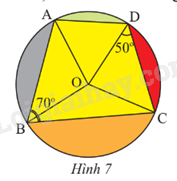
Trong hình vẽ minh họa của học sinh có một tứ giác ABCD nội tiếp đường tròn tâm O (Hình 7). Cho biết \(\widehat {ABC}\) = 70 o , \(\widehat {OCD}\) = 50 o . Tìm góc \(\widehat {AOD}\).
Phương pháp giải:
Dựa vào: Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180 o .
Lời giải chi tiết:
Tứ giác ABCD là tứ giác nội tiếp.
Do đó \(\widehat {ABC} + \widehat {ADC} = {180^o}\) suy ra \(\widehat {ADC} = {180^o} - \widehat {ABC} = {180^o} - {70^o} = {110^o}\).
Mà \(\widehat {ADO} + \widehat {OCD} = \widehat {ADC}\) suy ra \(\widehat {ADO} = {110^o} - {50^o} = {60^o}\).
Vì OA = OD = R nên tam giác OAD cân tại O
Suy ra \(\widehat {OAD} = \widehat {ADO} = {60^o}\) (tính chất tam giác cân)
Vậy tam giác OAD đều suy ra \(\widehat {AOD} = {60^o}\).