Giải mục 2 trang 85, 86 SGK Toán 9 tập 2 - Chân trời sáng tạo
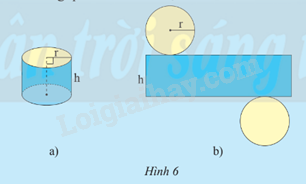
Hình khai triển của một hình trụ có bán kính đáy r, chiều cao h (Hình 6a) gồm hai hình tròn và một hình chữ nhật (Hình 6b). Diện tích của hình chữ nhật trong Hình 6b được gọi là diện tích xung quanh của hình trụ Hãy tính diện tích xung quanh của hình trụ theo r và h.
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 85 SGK Toán 9 Chân trời sáng tạo
Hình khai triển của một hình trụ có bán kính đáy r, chiều cao h (Hình 6a) gồm hai hình tròn và một hình chữ nhật (Hình 6b). Diện tích của hình chữ nhật trong Hình 6b được gọi là diện tích xung quanh của hình trụ
Hãy tính diện tích xung quanh của hình trụ theo r và h.
Phương pháp giải:
Dựa vào diện tích của hình chữ nhật rồi biến đổi theo h và r
Lời giải chi tiết:
Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh\)
VD
Trả lời câu hỏi Vận dụng trang 86 SGK Toán 9 Chân trời sáng tạo
Một nhà máy dự định sản xuất thùng phuy đựng dầu nhớt dạng hình trụ có đường kính đáy 0,6 m và chiều cao 0,9 m (Hình 7). Bỏ qua diện tích các mép thùng, hãy tính diện tích thép cần để sản xuất 100 thùng phuy như vậy (kết quả làm tròn đến hàng phần trăm).

Phương pháp giải:
- Dựa vào Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh\)
- Diện tích toàn phần \({S_{tp}} = {S_{xq}} + {S_{day}}\) để tính.
Lời giải chi tiết:
Diện tích thép xung quanh cần để sản xuất 1 thùng phuy là:
\({S_{xq}} = 2\pi rh = \pi dh\) = \(\pi \).0,6.0,9 = 0,54\(\pi \) (m 2 )
Diện tích toàn phần của 1 thùng phi là:
\({S_{tp}} = {S_{xq}} + {S_{day}} = 0,54\pi + 2.{\left( {\frac{{0,6}}{2}} \right)^2}.\pi = 0,72\pi \) (m 2 )
Diện tích thép cần để sản xuất 100 thùng phuy là:
S = 100. 0,72\(\pi \) = 226,19 (m 2 )
Vậy diện tích thép cần để sản xuất 100 thùng phuy là 226,19 m 2 .