Giải mục 2 trang 95, 96 SGK Toán 9 tập 2 - Chân trời sáng tạo
Nhà khoa học cổ đại Archimèdes đã khám phá ra cách tính diện tích của mặt cầu như sau: Lấy một nửa hình cầu bán kính R và một hình trụ có bán kính đáy R. Dùng sợi dây quấn quanh nửa mặt cầu như Hình 10a, rồi cùng đoạn dây đó người ta quấn quanh hình trụ như Hình 10b thì thấy chiều cao của phần hình trụ được quấn dây bằng bán kính R. a) Tính theo R diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b. b) Từ đó dự đoán diện tích nửa mặt cầu ở Hình 10a.
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 95 SGK Toán 9 Chân trời sáng tạo
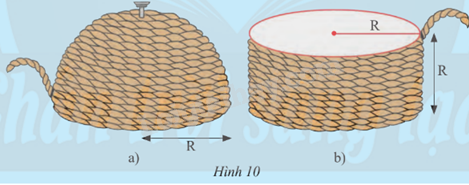
Nhà khoa học cổ đại Archimèdes đã khám phá ra cách tính diện tích của mặt cầu như sau: Lấy một nửa hình cầu bán kính R và một hình trụ có bán kính đáy R. Dùng sợi dây quấn quanh nửa mặt cầu như Hình 10a, rồi cùng đoạn dây đó người ta quấn quanh hình trụ như Hình 10b thì thấy chiều cao của phần hình trụ được quấn dây bằng bán kính R.
a) Tính theo R diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b.
b) Từ đó dự đoán diện tích nửa mặt cầu ở Hình 10a.
Phương pháp giải:
Dựa vào công thức tính diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh\)
Lời giải chi tiết:
a) Diện tích xung quanh của phần hình trụ là: S cầu = S trụ = \(2\pi {R^2}\)
b) Diện tích nửa mặt cầu là: S = S trụ = \(2\pi {R^2}\)
VD2
Trả lời câu hỏi Vận dụng 2 trang 96 SGK Toán 9 Chân trời sáng tạo
Tìm diện tích bề mặt của Mặt Trăng, biết đường kính Mặt Trăng là khoảng
3474 km.
Phương pháp giải:
Dựa vào công thức tính diện tích mặt cầu là: S = \(4\pi {R^2}\)
Lời giải chi tiết:
Bán kính Mặt Trăng là: \(R = \frac{d}{2} = \frac{{3474}}{2}\) = 1737 km.
Diện tích bề mặt của Mặt Trăng là:
S = \(4\pi {R^2} = 4\pi .{(1737)^2} \approx \) 37914864 km 2 .