Giải mục 2 trang 90 SGK Toán 9 tập 2 - Chân trời sáng tạo
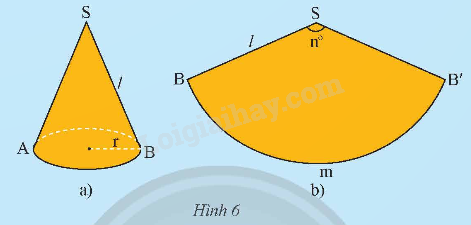
Cho một hình nón có bán kính r, có độ dài đường sinh l (Hình 6a). Cắt mặt xung quanh của hình nón theo một đường sinh của nó rồi trải phẳng ra, ta được hình quạt tròn (Hình 6b). Tính theo r và l: a) Độ dài cung BB’; b) Số đo cung BB’; c) Diện tích của hình quạt tròn.
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 90 SGK Toán 9 Chân trời sáng tạo
Cho một hình nón có bán kính r, có độ dài đường sinh l (Hình 6a). Cắt mặt xung quanh của hình nón theo một đường sinh của nó rồi trải phẳng ra, ta được hình quạt tròn (Hình 6b). Tính theo r và l:
a) Độ dài cung BB’;
b) Số đo cung BB’;
c) Diện tích của hình quạt tròn.
Phương pháp giải:
Dựa vào tính độ dài cung, số đo cung và diện tích biểu diễn theo r và l.
Lời giải chi tiết:
a) Độ dài cung BB’ là: m = 2\(\pi \)r.
b) Số đo cung BB’ là: \(m = \frac{{\pi \ln }}{{180}}\) suy ra \(n = \frac{{180.m}}{{\pi {\mathop{\rm l}\nolimits} }}\).
c) Diện tích của hình quạt tròn là:
\(S = \frac{{n\pi {l^2}}}{{360}} = \frac{{\pi {l^2}}}{{360}}.\frac{{180.m}}{{\pi l}} = \frac{{l.m}}{2} = \frac{{2\pi rl}}{2} = \pi rl\).
TH3
Trả lời câu hỏi Thực hành 3 trang 90 SGK Toán 9 Chân trời sáng tạo
Tính diện tích xung quanh và diện tích toàn phần của hình nón có đường kính đáy d = 10 m và chiều cao h = 12 m (kết quả làm tròn đến hàng phần trăm).
Phương pháp giải:
- Dựa vào diện tích xung quanh của hình nón có bán kính r, độ dài đường sinh l là: \({S_{xq}} = \pi rl\)
- Diện tích toàn phần \({S_{tp}} = {S_{xq}} + {S_{day}}\) để tính.
Lời giải chi tiết:
Ta có \(l = \sqrt {{r^2} + {h^2}} \) = 13 m.
Diện tích xung quanh là: \({S_{xq}} = \pi rl = \pi .5.13\) = 204,20 m 2 .
Diện tích toàn phần là:
\({S_{tp}} = {S_{xq}} + {S_{day}} = 204,20 + \pi {r^2} = 204,20 + \pi {.5^2}\) = 282, 74 m 2 .