Giải mục 2 trang 70 SGK Toán 7 tập 1 - Chân trời sáng tạo
Cho hai đường thẳng xy và zt cắt nhau tại O (Hình 7). Ta gọi tia Oy là tia đối của tia Ox và gọi tia Ot là tia đối của tia Oz. ...a) Vẽ hai đường thẳng ab và cd cắt nhau tại điểm I. Xác định các cặp góc đối đỉnh trên hình vẽ
HĐ 2
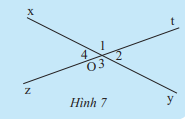
Cho hai đường thẳng xy và zt cắt nhau tại O (Hình 7). Ta gọi tia Oy là tia đối của tia Ox và gọi tia Ot là tia đối của tia Oz. Hãy cho biết quan hệ về cạnh, quan hệ về đỉnh của \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) .
Phương pháp giải:
Xác định các cạnh và đỉnh của các góc \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\).
Lời giải chi tiết:
\(\widehat {{O_1}}\) có cạnh Ox và Ot, đỉnh O
\(\widehat {{O_3}}\) có cạnh Oy và Oz, đỉnh O
Ta có: \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có chung đỉnh
Thực hành 2
a) Vẽ hai đường thẳng ab và cd cắt nhau tại điểm I. Xác định các cặp góc đối đỉnh trên hình vẽ
b) Vẽ \(\widehat {xOy}\) rồi vẽ \(\widehat {tOz}\) đối đỉnh với \(\widehat {xOy}\)
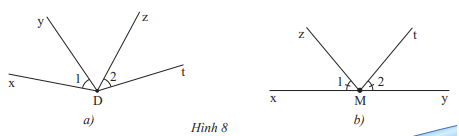
c) Cặp góc \(\widehat {xDy}\) và \(\widehat {zDt}\) trong Hình 8a và cặp góc \(\widehat {xMz}\) và \(\widehat {tMy}\) trong Hình 8b có phải là các cặp góc đối đỉnh hay không? Hãy giải thích tại sao.
Phương pháp giải:
Vẽ hình
Hai góc đối đỉnh là hai góc có chung gốc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
Lời giải chi tiết:
a)
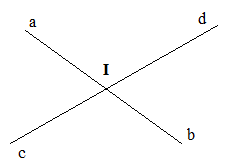
Các cặp góc đối đỉnh trên hình vẽ là: \(\widehat {aId}\) và \(\widehat {bIc}\); \(\widehat {aIc}\) và \(\widehat {bId}\)
b)
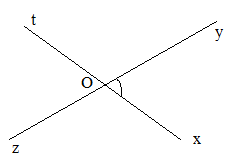
Bước 1: Vẽ góc \(\widehat {xOy}\)
Bước 2: Vẽ tia Ot là tia đối của tia Ox
Bước 3: Vẽ tia Oz là tia đối của tia Oy
Ta được \(\widehat {tOz}\) đối đỉnh với \(\widehat {xOy}\)
c) Cặp góc \(\widehat {xDy}\) và \(\widehat {zDt}\) trong Hình 8a và cặp góc \(\widehat {xMz}\) và \(\widehat {tMy}\) trong Hình 8b không phải là các cặp góc đối đỉnh vì mỗi cạnh của góc này không là cạnh đối của một cạnh của góc kia
Ở Hình 8a, Dt không là tia đối của Dx hay Dy; Dz không là tia đối của Dx hay Dy
Ở Hình 8b, My là tia đối của Mx nhưng Mt không là tia đối của Mz
Chú ý: 2 đường thẳng cắt nhau tạo ra 2 cặp góc đối đỉnh
Vận dụng 2
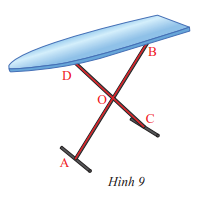
Hai chân chống AB và CD của cái bàn xếp ở Hình 9 cho ta hình ảnh hai đường thẳng cắt nhau tại điểm O. Hãy chỉ ra các góc đối đỉnh trong hình
Phương pháp giải:
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia
Lời giải chi tiết:
Các góc đối đỉnh trong hình là: \(\widehat {DOB}\) và \(\widehat {COA}\); \(\widehat {BOC}\) và \(\widehat {AOD}\)