Giải mục 2 trang 8, 9 SGK Toán 10 tập 2 - Chân trời sáng tạo — Không quảng cáo

HĐ Khám phá 2

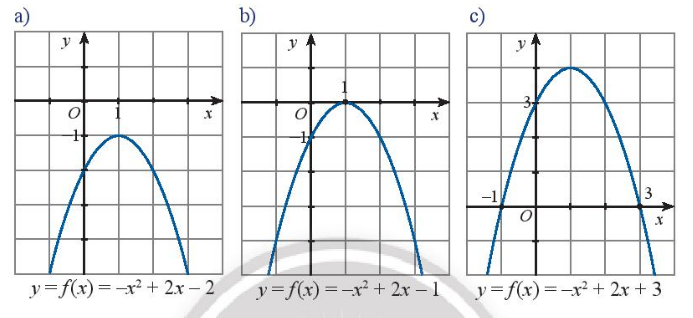
Quan sát đồ thị của các hàm số bậc hai trong các hình thức dưới đây. Trong mỗi trường hợp, hãy cho biết:

+) Các nghiệm (nếu có) và dấu của biệt thức $\Delta$

+) Các khoảng giá trị của $x$mà trên đó $f\left( x \right)$ cùng dấu với hệ số của ${x^2}$

Phương pháp giải:

Bước 1: Xác định nghiệm của hàm số là giao của đồ thị và trục hoành

Bước 2: Xác định biệt thức $\Delta  = {b^2} - 4ac$ và xác định dấu của nó

Bước 3: Dựa vào đồ thị xác định dấu của $f\left( x \right)$

+) Phần đồ thị nằm trên trục hoành là $f\left( x \right) > 0$

+) Phần đồ thị nằm dưới trục hoành là $f\left( x \right) < 0$

Lời giải chi tiết:

a) Dựa vào đồ thị ta thấy hàm số đã cho vô nghiệm

Biệt thức $\Delta  = {2^2} - 4.\left( { - 1} \right).\left( { - 2} \right) =  - 4 < 0$

Ta thấy hệ số của ${x^2}$ là $- 1 < 0$

Đồ thị nằm dưới trục hoành với mọi x

Nên $f\left( x \right)$ cùng dấu với hệ số của ${x^2}$ với $\forall x \in \mathbb{R}$

b) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép ${x_1} = {x_2} = 1$

Biệt thức $\Delta  = {2^2} - 4.\left( { - 1} \right).\left( { - 1} \right) = 0$

Ta thấy hệ số của ${x^2}$ là $- 1 < 0$

Đồ thị nằm dưới trục hoành với mọi x

Nên $f\left( x \right)$ cùng dấu với hệ số của ${x^2}$ với $\forall x \in \mathbb{R}$

c) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt  ${x_1} =  - 1;{x_2} = 3$

Biệt thức $\Delta  = {2^2} - 4.\left( { - 1} \right).3 = 16 > 0$

Ta thấy hệ số của ${x^2}$ là $- 1 < 0$

Đồ thị nằm dưới trục hoành khi  $x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)$

Đồ thị nằm trên trục hoành với mọi $x \in \left( { - 1,3} \right)$

Nên $f\left( x \right)$ cùng dấu với hệ số của ${x^2}$ khi $x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)$

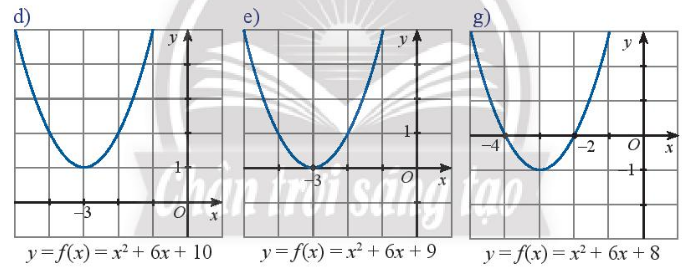
d) Dựa vào đồ thị ta thấy hàm số bậc hai đã cho vô nghiệm

Biệt thức $\Delta  = {6^2} - 4.1.10 =  - 4 < 0$

Ta thấy hệ số của ${x^2}$ là $1 > 0$

Đồ thị nằm trên trục hoành với mọi $x$

Nên $f\left( x \right)$ cùng dấu với hệ số của ${x^2}$ với mọi $x \in \mathbb{R}$

e) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép ${x_1} = {x_2} =  - 3$

Biệt thức $\Delta  = {6^2} - 4.1.9 = 0$

Ta thấy hệ số của ${x^2}$ là $1 > 0$

Đồ thị nằm trên trục hoành với mọi x

Nên $f\left( x \right)$ cùng dấu với hệ số của ${x^2}$ với mọi $x \in \mathbb{R}$

g) ) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt  ${x_1} =  - 4;{x_2} =  - 2$

Biệt thức $\Delta  = {6^2} - 4.1.8 = 4 > 0$

Ta thấy hệ số của ${x^2}$ là $1 > 0$

Đồ thị nằm trên trục hoành khi  $x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)$

Đồ thị nằm dưới trục hoành với mọi $x \in \left( { - 4, - 2} \right)$

Nên $f\left( x \right)$ cùng dấu với hệ số của ${x^2}$ khi $x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)$

Thực hành 3

Xét dấu của các tam thức bậc hai sau:

a) $f\left( x \right) = 2{x^2} - 3x - 2$

b) $g\left( x \right) =  - {x^2} + 2x - 3$

Phương pháp giải:

Bước 1: Tính và xác định dấu của biệt thức $\Delta  = {b^2} - 4ac$

Bước 2: Xác định nghiệm của $f\left( x \right)$ (nếu có) $x = \frac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$

Bước 3: Xác định dấu của hệ số $a$

Bước 4: Xác định dấu của $f\left( x \right)$

Lời giải chi tiết:

a) $f\left( x \right) = 2{x^2} - 3x - 2$ có $\Delta  = 25 > 0$, hai nghiệm phân biệt là ${x_1} =  - \frac{1}{2};{x_2} = 2$

và $a = 2 > 0$

Ta có bảng xét dấu như sau:

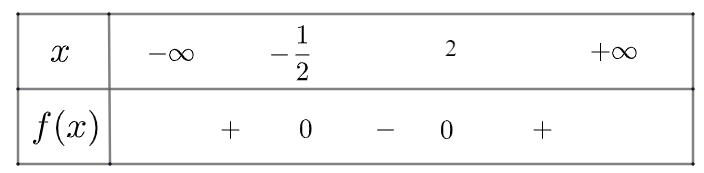
Vậy $f\left( x \right)$ âm trong khoảng $\left( { - \frac{1}{2},2} \right)$ và dương trong hai khoảng

$\left( { - \infty , - \frac{1}{2}} \right)$ và $\left( {2, + \infty } \right)$

b) $g\left( x \right) =  - {x^2} + 2x - 3$ có $\Delta  = {2^2} - 4.\left( { - 1} \right).\left( { - 3} \right) =  - 8 < 0$ và $a =  - 1 < 0$

Vậy $g\left( x \right)$âm với mọi $x \in \mathbb{R}$

Vận dụng

Xét dấu tam thức bậc hai $h\left( x \right) =  - 0,006{x^2} + 1,2x - 30$ trong bài toán khởi động và cho biết ở khoảng cách nào tính từ đầu cầu O thì vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu

Phương pháp giải:

Bước 1: Tính và xác định dấu của biệt thức $\Delta  = {b^2} - 4ac$

Bước 2: Xác định nghiệm của $h\left( x \right)$ (nếu có) $x = \frac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$

Bước 3: Xác định dấu của hệ số $a$

Bước 4: Xác định dấu của $h\left( x \right)$

Lời giải chi tiết:

$h\left( x \right) =  - 0,006{x^2} + 1,2x - 30$ có $\Delta  = 1,{2^2} - 4.\left( { - 0,006} \right).\left( { - 30} \right) = \frac{{18}}{{25}} > 0$, hai nghiệm phân biệt là ${x_1} = 100 - 50\sqrt 2 ;{x_2} = 100 + 50\sqrt 2$ và $a =  - 0,006 < 0$

Ta có bảng xét dấu $h\left( x \right)$ như sau:

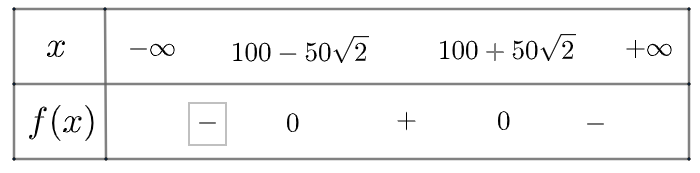
Vậy vòm cầu cao hơn mặt cầu là khoảng cách từ $100 - 50\sqrt 2$(m) đến $100 + 50\sqrt 2$ (m) (cách từ O), vòm vòm cầu thấp hơn mặt cầu là khoảng cách từ O đến$100 - 50\sqrt 2$(m) và từ $100 + 50\sqrt 2$ (m) đến 200 (m) (cách từ O)