Giải mục 3 trang 101 SGK Toán 9 tập 1 - Chân trời sáng tạo
a) Vẽ đường tròn (C) tâm O bán kính r = 5 cm và đường tròn (C’) tâm O bán kính R = 8 cm. b) Tính diện tích S của (C) và diện tích S’ của (C’). c) Hãy cho biết hiệu số (S’ – S) biểu diễn diện tích của phần nào trên Hình 9.
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 101 SGK Toán 9 Chân trời sáng tạo
a) Vẽ đường tròn (C) tâm O bán kính r = 5 cm và đường tròn (C’) tâm O bán kính R = 8 cm.
b) Tính diện tích S của (C) và diện tích S’ của (C’).
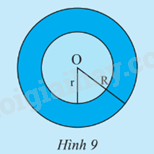
c) Hãy cho biết hiệu số (S’ – S) biểu diễn diện tích của phần nào trên Hình 9.
Phương pháp giải:
- Đọc kĩ dữ kiện để vẽ hình.
- Dựa vào công thức diện tích đường tròn S =\(\pi \)R 2
Lời giải chi tiết:
a) Ta có hình vẽ:
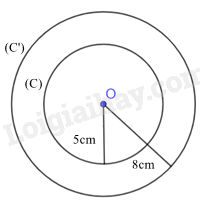
b) Diện tích S của (C) là: \(S = 5^2\pi = 25\pi \approx 78,54 (cm^2)\)
Diện tích S’ của (C’) là \(S’ = 8^2\pi = 64\pi \approx 201,06 (cm^2)\)
c) Hiệu số (S’ – S) biểu diễn diện tích của phần tô màu xanh đậm trong hình 9.
TH3
Trả lời câu hỏi Thực hành 3 trang 101 SGK Toán 9 Chân trời sáng tạo
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) (kết quả làm tròn đến hàng phần trăm)
Phương pháp giải:
- Đọc kĩ dữ kiện để vẽ hình.
- Áp dụng diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) là: \(S = \pi ({R^2} - {r^2})\)
Lời giải chi tiết:
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) là:
\(S = \pi ({R^2} - {r^2}) = \pi ({20^2} - {10^2}) = 300\pi \approx 942,48\) cm 2 .
VD3
Trả lời câu hỏi Vận dụng 3 trang 101 SGK Toán 9 Chân trời sáng tạo
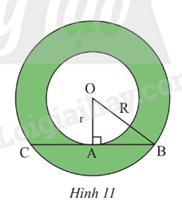
Cho hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) với R > r. Trên đường tròn (O; R) lấy hai điểm B, C sao cho BC vừa là dây cung của (O; R), vừa là tiếp tuyến của đường tròn (O; r) tại A (Hình 11)
a) Tính độ dài đoạn thẳng BC theo r và R.
b) Cho BC = \(a\sqrt 3 \). Tính diện tích hình khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a.
Phương pháp giải:
- Dựa vào tính chất tiếp tuyến chứng minh OA \( \bot \)BC
- Tính BC bằng cách áp dụng định lý pythagore trong tam giác vuông
- Áp dụng diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) là: \(S = \pi ({R^2} - {r^2})\)
Lời giải chi tiết:
a) Vì BC là tiếp tuyến của đường tròn (O; r) tại A nên OA \( \bot \)BC
Xét tam giác OAB vuông tại A , ta có:
AB = \(\sqrt {O{B^2} - O{A^2}} = \sqrt {{R^2} - {r^2}} \) (theo định lý Pythagore)
Tương tự với tam giác OCA vuông tại A, ta có
AC = \(\sqrt {O{C^2} - O{A^2}} = \sqrt {{R^2} - {r^2}} \) (theo định lý Pythagore)
Vậy BC = AB + AC = 2\(\sqrt {{R^2} - {r^2}} \).
b) Ta có BC = 2\(\sqrt {{R^2} - {r^2}} \) = \(a\sqrt 3 \) suy ra \(\sqrt {{R^2} - {r^2}} \) = \(\frac{{a\sqrt 3 }}{2}\)
Diện tích hình khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a là:
\(S = \pi ({R^2} - {r^2})\) = \(\pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = \frac{{3\pi }}{4}{a^2}\).