Giải mục 3 trang 18 SGK Toán 7 tập 1 - Kết nối tri thức
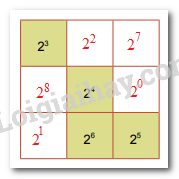
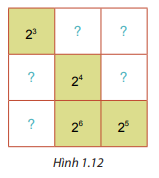
Viết số 2^2^3 dưới dạng lũy thừa cơ số 2 ....Viết các số ...Cho hình vuông như Hình 1.12. Em hãy thay mỗi dấu “?” bằng một lũy thừa của 2, biết các lũy thừa trên mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau.
HĐ 5
Viết số \({({2^2})^3}\) dưới dạng lũy thừa cơ số 2 và số \({\left[ {{{( - 3)}^2}} \right]^2}\) dưới dạng lũy thừa cơ số \(-3\).
Phương pháp giải:
Sử dụng định nghĩa lũy thừa và công thức tích các lũy thừa có cùng cơ số
Lời giải chi tiết:
Ta có: +) \({({2^2})^3} = {2^2}{.2^2}{.2^2} = {2^{2 + 2 + 2}} = {2^6}\)
+) \({\left[ {{{( - 3)}^2}} \right]^2} = {( - 3)^2}.{( - 3)^2} = {( - 3)^{2 + 2}} = {( - 3)^4}\)
Luyện tập 4
Viết các số \({\left( {\frac{1}{4}} \right)^8};{\left( {\frac{1}{8}} \right)^3}\) dưới dạng lũy thừa cơ số \(\frac{1}{2}\)
Phương pháp giải:
+ Bước 1: Viết các số \(\frac{1}{4};\frac{1}{8}\) dưới dạng lũy thừa cơ số \(\frac{1}{2}\)
+ Bước 2: Sử dụng công thức lũy thừa của lũy thừa: \({({x^m})^n} = {x^{m.n}}\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}{\left( {\frac{1}{4}} \right)^8} = {[{\left( {\frac{1}{2}} \right)^2}]^8} = {(\frac{1}{2})^{2.8}} = {(\frac{1}{2})^{16}};\\{\left( {\frac{1}{8}} \right)^3} = {[{(\frac{1}{2})^3}]^3} = {(\frac{1}{2})^{3.3}} = {(\frac{1}{2})^9}\end{array}\)
Thử thách nhỏ
Cho hình vuông như Hình 1.12. Em hãy thay mỗi dấu “?” bằng một lũy thừa của 2, biết các lũy thừa trên mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau.
Phương pháp giải:
Tính tích của 3 ô in đậm ở đường chéo đã biết. Tích này chính là tích của từng hàng , cột.
Tính hàng, cột khi biết tích của hàng, cột và 2 ô của hàng, cột đó.
Lời giải chi tiết:
Ta đặt các ô chưa biết như sau:
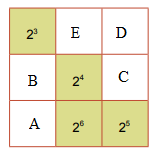
Ta có:
Tích của mỗi hàng, cột, đường chéo bằng: \({2^3}{.2^4}{.2^5} = {2^{3 + 4 + 5}} = {2^{12}}\)
\(\begin{array}{l}A = {2^{12}}:{2^6}:{2^5} = {2^{12 - 6 - 5}} = {2^1} = 2;\\B = {2^{12}}:{2^1}:{2^3} = {2^{12 - 1 - 3}} = {2^8};\\C = {2^{12}}:{2^8}:{2^4} = {2^{12 - 8 - 4}} = {2^0} = 1;\\D = {2^{12}}:{2^0}:{2^5} = {2^{12 - 0 - 5}} = {2^7};\\E = {2^{12}}:{2^7}:{2^3} = {2^{12 - 7 - 3}} = {2^2}\end{array}\)
Vậy ta có bảng hoàn chỉnh là: