Giải mục 3 trang 28, 29, 30 SGK Toán 9 tập 2 - Cánh diều
Xét mẫu số liệu được ghép nhóm ở Hoạt động 2 với bảng tần số ghép nhóm là Bảng 27: Tính tỉ số phần trăm của tần số ({n_1} = 5) và N=40?
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 28 SGK Toán 9 Cánh diều
Xét mẫu số liệu được ghép nhóm ở Hoạt động 2 với bảng tần số ghép nhóm là Bảng 27 :

Tính tỉ số phần trăm của tần số \({n_1} = 5\)và N=40?
Phương pháp giải:
Tỉ số phần trăm của số a và số b là \(\frac{a}{b}.100\% \)
Lời giải chi tiết:
Tỉ số phần trăm của tần số \({n_1} = 5\)và N=40 là \(\frac{5}{{40}}.100\% = 12,5\% \)
LT3
Trả lời câu hỏi Luyện tập 3 trang 30 SGK Toán 9 Cánh diều
Xét mẫu số liệu sau khi được ghép nhóm ở Luyện tập 2. Lập bảng tần số tương đối ghép nhóm của mẫu số liệu đó.

Phương pháp giải:
Tính tỉ số phần trăm của mỗi tần số.
Lời giải chi tiết:
Tần số tương đối của các nhóm lần lượt là:
\(\begin{array}{l}{f_1} = \frac{5}{{30}}.100\% = 16,7\% ;{f_2} = \frac{6}{{30}}.100\% = 20\% ;{f_3} = \frac{6}{{30}}.100\% = 20\% ;\\{f_4} = \frac{4}{{30}}.100\% = 13,3\% ;{f_5} = \frac{3}{{30}}.100\% = 10\% ;{f_6} = \frac{6}{{30}}.100\% = 20\% \end{array}\)
Ta có bảng:

HĐ4
Trả lời câu hỏi Hoạt động 4 trang 30 SGK Toán 9 Cánh diều
Xét mẫu số liệu ghép nhóm ở Ví dụ 3 với bảng tần số tương đối ghép nhóm là Bảng 33.
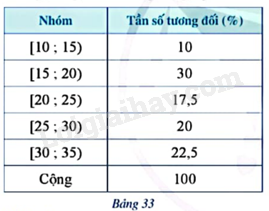
a) Vẽ 2 trục vuông góc với nhau.
b) Trên trục nằm ngang, ta xác định các điểm 10, 15, 20, 25, 30, 35 (các điểm cách đều nhau.
Trên trục thẳng đứng ta xác định độ dài đơn vị và đánh dấu các điểm biểu diễn tần số tương đối của nhóm.
Trên mỗi nửa khoảng [10; 15), [15; 20), [25; 30), [30; 35) của trục nằm ngang (ứng với 5 nhóm đã cho), vẽ một cột hình chữ nhật có chiều cao thể hiện tần số tương đối của nhóm đó.
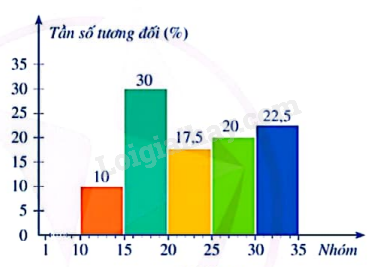
c) Hoàn thiện biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột biểu diễn số liệu thống kê trong Bảng 33.
Phương pháp giải:
Thực hiện lần lượt từng yêu cầu của đề bài.
Lời giải chi tiết:
HĐ5
Trả lời câu hỏi Hoạt động 5 trang 32 SGK Toán 9 Cánh diều
Xét mẫu số liệu ghép nhóm ở Ví dụ 4 với bảng tần số tương đối ghép nhóm là Bảng 34.

Trên mặt phẳng hãy:
a) Xác định đầu mút trái, đầu mút phải, tần số tương đối \({f_1}\) của nhóm 1 ứng với nửa khoảng [0; 20). Từ đó xác định điểm \({M_1}({c_1};{f_1})\), trong đó \({c_1}\)là trung bình cộng hai đầu mút của nhóm 1.
b) Bằng cách tương tự, xác định các điểm \({M_2}({c_2};{f_2}),{M_3}({c_3};{f_3}),{M_4}({c_4};{f_4}),{M_5}({c_5};{f_5})\), trong đó \({c_2},{c_3},{c_4},{c_5}\)lần lượt là trung bình cộng hai đầu mút của nhóm 2, 3, 4, 5.
c) Vẽ đường gấp khúc \({M_1}{M_2}{M_3}{M_4}{M_5}\).
Phương pháp giải:
Nhóm 1: tần số tương đối \({f_1} = 10\% \), \({c_1} = \frac{{0 + 20}}{2} = 10\) đầu mút trái là 0, đầu mút phải là 20.
Tượng tự đối với các nhóm còn lại.
Lời giải chi tiết:
a) Đầu mút trái: 0; đầu mút phải: 20
\(f_1 = 10%\)
\(M_1(10; 10)\)
b) \(M_2(30;15)\); \(M_3(50;30)\)
\(M_4(70;35)\); \(M_5(90;10)\)

LT4
Trả lời câu hỏi Luyện tập 4 trang 33 SGK Toán 9 Cánh diều
Bảng 36 là bảng tần số tương đối ghép nhóm của một mẫu số liệu ghép nhóm.
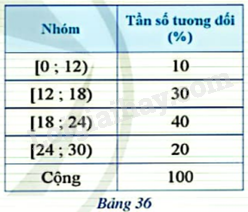
Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và ở dạng biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.
Phương pháp giải:
Biểu đồ cột: trục nằm ngang thể hiện các số liệu của các nhóm, trục thẳng đứng thể hiện tần số tương đối.
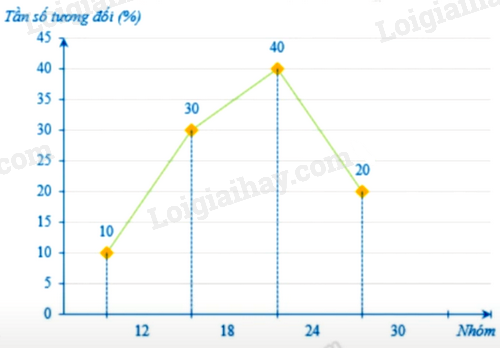
Biểu đồ đoạn thẳng: xác định các điểm \({M_1}({c_1};{f_1})\),\({M_2}({c_2};{f_2}),{M_3}({c_3};{f_3}),{M_4}({c_4};{f_4})\)trong đó \({c_1},{c_2},{c_3},{c_4}\)lần lượt là trung bình cộng hai đầu mút của nhóm 1, 2, 3, 4.
Lời giải chi tiết:
Biểu đồ cột:
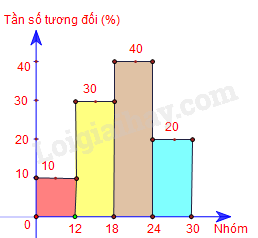
Biểu đồ đoạn thẳng: