Giải mục 2 trang 108, 109 SGK Toán 9 tập 1 - Cánh diều — Không quảng cáo

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 108 SGK Toán 9 Cánh diều

Cho đường tròn \(\left( {O;R} \right)\). Các đường thẳng \(c,d\) lần lượt tiếp xúc với đường tròn \(\left( {O;R} \right)\) tại \(A,B\) và cắt nhau tại \(M\) (Hình 38).

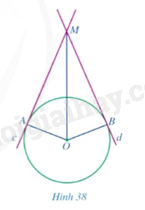
a) Các tam giác \(MOA\) và \(MOB\) có bằng nhau hay không?

b) Hai đoạn thẳng \(MA\) và \(MB\) có bằng nhau hay không?

c) Tia \(MO\) có phải là tia phân giác của góc \(AMB\) hay không?

d) Tia \(OM\) có phải là tia phân giác của góc \(AOB\) hay không?

Phương pháp giải:

Dựa vào tam giác bằng nhau để chứng minh.

Lời giải chi tiết:

a) Do \(MA\) là tiếp tuyến của \(\left( {O;R} \right)\) nên \(MA \bot AO\) suy ra \(\widehat {MAO} = 90^\circ \).

Do \(MB\) là tiếp tuyến của \(\left( {O;R} \right)\) nên \(MB \bot BO\) suy ra \(\widehat {MBO} = 90^\circ \).

Xét tam giác \(MOA\)và tam giác \(MOB\) có:

\(\widehat {MAO} = \widehat {MBO} = 90^\circ \)

\(OA = OB = R\)

\(OM\) chung

\( \Rightarrow \Delta MOA = \Delta MOB\) (cạnh huyền – cạnh góc vuông).

b) Do \(\Delta MOA = \Delta MOB\) nên \(MA = MB\) (2 cạnh tương ứng).

c) Do \(\Delta MOA = \Delta MOB\) nên \(\widehat {AMO} = \widehat {BMO}\) (2 góc tương ứng) suy ra \(MO\) là tia phân giác của góc \(AMB\).

d) Do \(\Delta MOA = \Delta MOB\) nên \(\widehat {MOA} = \widehat {MOB}\) (2 góc tương ứng) suy ra \(OM\) là tia phân giác của góc \(AOB\).

LT4

Trả lời câu hỏi Luyện tập 4 trang 109 SGK Toán 9 Cánh diều

Cho đường tròn \(\left( {O;R} \right)\) và điểm \(M\) nằm ngoài đường tròn. Hai đường thẳng \(c,d\) qua \(M\) lần lượt tiếp xúc với \(\left( O \right)\) tại \(A,B\) biết \(\widehat {AMB} = 120^\circ \). Chứng minh \(AB = R\).

Phương pháp giải:

Dựa vào tính chất 2 tiếp tuyến cắt nhau và tỉ số lượng giác để làm bài toán.

Lời giải chi tiết:

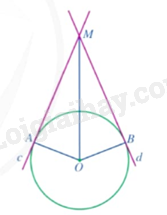
Cách 1.

Vì \(MA,MB\) là các tiếp tuyến của \(\left( O \right)\) nên MO là tia phân giác của góc AMB, suy ra \(\widehat {AMO} = \widehat {BMO} = \frac{{\widehat {AMB}}}{2} = 60^\circ \).

Xét tam giác \(AMO\) vuông tại \(A\) có:

\(\widehat {AMO} + \widehat {MOA} = 90 \\60^\circ  + \widehat {MOA} = 90^\circ \\ \widehat {MOA} = 30^\circ \)

Vì \(MA,MB\) là các tiếp tuyến của \(\left( O \right)\) nên OM là tia phân giác của góc AOB, suy ra \(\widehat {AOB} = 2\widehat {AOM} = 2.30^\circ  = 60^\circ \).

Xét tam giác \(AOB\) có: \(OA = OB = R\) nên tam giác \(AOB\) cân tại \(O\).

Lại có \(\widehat {AOB} = 60^\circ \) suy ra tam giác \(AOB\) là tam giác đều.

Vậy \(AO = OB = AB = R\).

Cách 2.

Vì MA, MB là tiếp tuyến của \((O)\) nên \(MA \bot OA\), \(MB \bot OB\) suy ra \(\widehat {MAO} = \widehat {MBO} = 90^\circ \)

Xét tứ giác OAMB có:

\(\widehat {AMB} + \widehat {MAO} + \widehat {MBO} + \widehat {AOB} = 360^\circ \)

Suy ra \(\hat O = 360^\circ  - 120^\circ  - 90^\circ  - 90^\circ  = {60^\circ }\)

Xét \(\Delta OAB\) có \(OA = OB = R\) suy ra \(\Delta OAB\) cân tại \(O\)

Lại có \(\hat O = 60^\circ \) (cmt)

Suy ra \(\Delta OAB\) đều

Do đó \(OA = OB = AB = R\) (đpcm)