Giải Phần A. Tái hiện, củng cố trang 8 Bài tập phát triển năng lực Toán 5 tập 2
Trong các hình sau, hình nào là hình hộp chữ nhật, hình nào là hình lập phương? Tính diện tích mảnh đất có hình dạng và kích thước như hình vẽ bên.
Câu 1
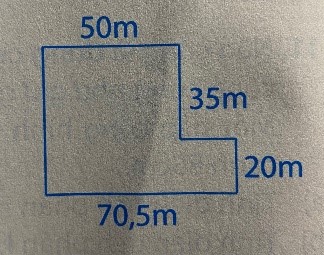
Tính diện tích mảnh đất có hình dạng và kích thước như hình vẽ bên.
Phương pháp giải:
Chia hình đã cho thành cách hình chữ nhật nhỏ.
Tính diện tích mỗi hình, từ đó tìm được diện tích mảnh đất ban đầu bằng cách tìm tổng diện tích các hình chữ nhật nhỏ.
Lời giải chi tiết:
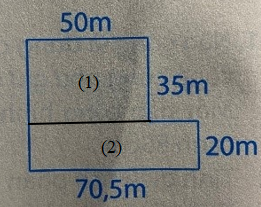
Chia hình vẽ thành hai hình chữ nhật là hình (1) và hình (2)
Diện tích hình chữ nhật (1) là:
50 x 35 = 1750 (m 2 )
Diện tích hình chữ nhật (2) là:
70,5 x 20 = 1410 (m 2 )
Diện tích mảnh đất là:
1750 + 1410 = 3160 (m 2 )
Đáp số: 3160 m 2
Câu 2
Tính chu vi và diện tích một sân bóng có hình dạng và kích thước như hình bên.

Phương pháp giải:
- Chu vi của sân vận động bằng chu vi hai nửa hình tròn cộng với hai lần chiều dài hình chữ nhật. - Diện tích sân bóng bằng = Diện tích hình tròn có đường kính 68m + diện tích hình chữ nhật
Lời giải chi tiết:
Chu vi của hai nửa hình tròn có đường kính 68 m là:
68 x 3,14 = 213,52 (m)
Hai lần chiều dài hình chữ nhật là
105 x 2 = 210 (m)
Chu vi sân bóng là:
213,52 + 210 = 423,52 (m)
Bán kính của hình tròn là
68 : 2 = 34 (m)
Diện tích hai nửa hình tròn là:
34 x 34 x 3,14 = 3629,84 (m 2 )
Diện tích sân bóng hình chữ nhật là:
105 x 68 = 7140 (m 2 )
Diện tích một sân bóng là:
3629,84 + 7140 = 10769,84(m 2 )
Đáp số: Chu vi: 423,52m
Diện tích: 10769,84m 2
Câu 3
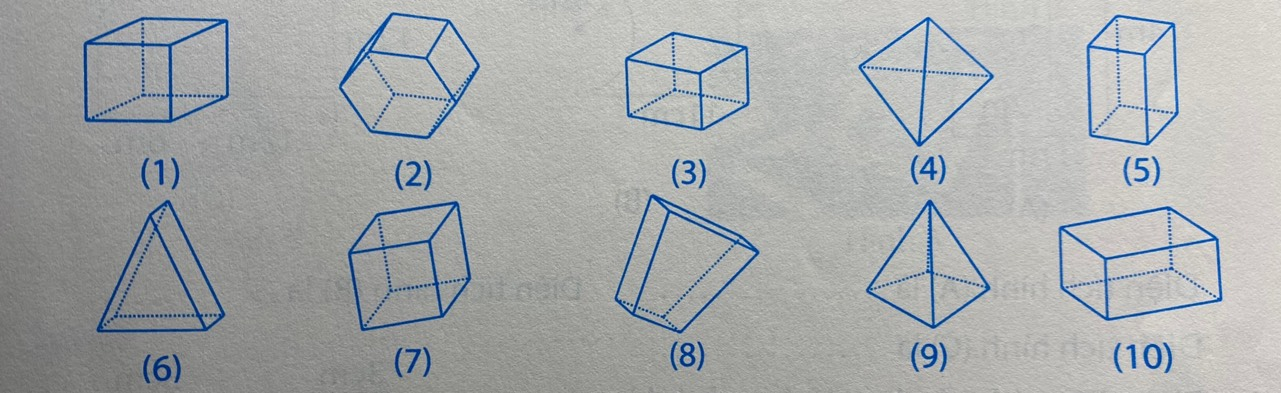
Trong các hình sau, hình nào là hình hộp chữ nhật, hình nào là hình lập phương?
Phương pháp giải:
Quan sát hình vẽ để trả lời câu hỏi.
Lời giải chi tiết:
- Các hình hộp chữ nhật là: (3); (5); (10)
- Các hình lập phương là: (1); (7)
Câu 4
Đúng ghi Đ, sai ghi S
a) Hình hộp chữ nhật có 4 đỉnh
b) Hình lập phương có 7 đỉnh
c) Hình hộp chữ nhật có 6 mặt là hình chữ nhật bằng nhau.
d) Hình lập phương có 6 mặt là 6 hình vuông bằng nhau.
e) Muốn tính diện tích xung quanh của hình hộp chữ nhật, ta lấy chu vi mặt đáy nhân với chiều cao
(cùng một đơn vị đo)
g) Muốn tính diện tích toàn phần của hình hộp chữ nhật, ta lấy diện tích một mặt nhân với 6.
Phương pháp giải:
- Hình hộp chữ nhật có 6 mặt là hình chữ nhật, 8 đỉnh, 12 cạnh
- Hình lập phương có 6 mặt là các hình vuông bằng nhau, 8 đỉnh, 12 cạnh
- Muốn tính diện tích xung quanh của hình hộp chữ nhật, ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo)
- Diện tích toàn phần của hình hộp chữ nhật = Diện tích xung quanh + diện tích 2 mặt đáy
Lời giải chi tiết:

Câu 5
Viết số đo thích hợp vào ô trống:
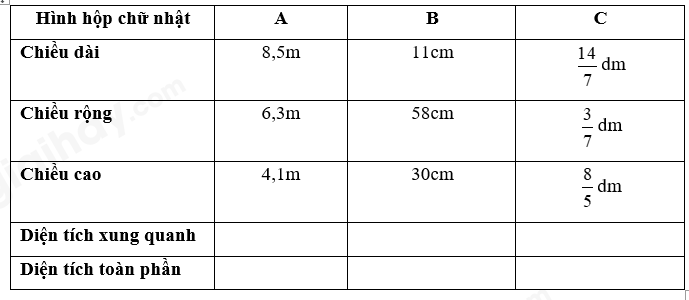
Phương pháp giải:
Áp dụng các công thức:
- Diện tích xung quanh = (chiều dài + chiều rộng) x 2 x chiều cao
- Diện tích toàn phần = diện tích xung quanh + diện tích hai đáy
Lời giải chi tiết:
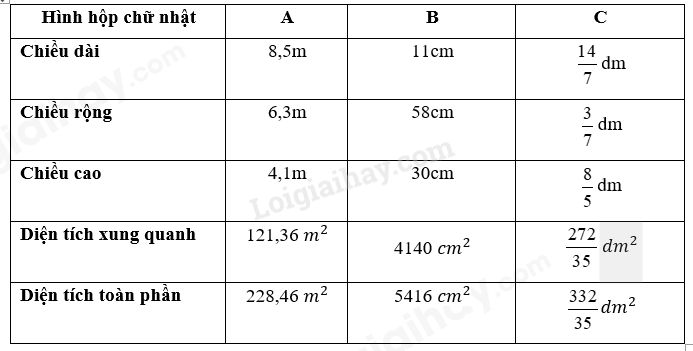
* Hình hộp chữ nhật A
Diện tích xung quanh là:
(8,5 + 6,3) x 2 x 4,1 = 121,36 (m 2 )
Diện tích mặt đáy là:
8,5 x 6,3 = 53,55 (m 2 )
Diện tích toàn phần là:
121,36 + 53,55 x 2 = 228,46 (m 2 )
* Hình hộp chữ nhật B
Diện tích xung quanh là:
(11 + 58) x 2 x 30 = 4140 (cm 2 )
Diện tích mặt đáy là:
11 x 58 = 638 (cm 2 )
Diện tích toàn phần là:
4140 + 638 x 2 = 5416 (cm 2 )
* Hình hộp chữ nhật C
Diện tích xung quanh là:
$\left( {\frac{{14}}{7} + \frac{3}{7}} \right) \times 2 \times \frac{8}{5} = \frac{{272}}{{35}}$ (dm 2 )
Diện tích mặt đáy là:
$\frac{{14}}{7} \times \frac{3}{7} = \frac{6}{7}$ (dm 2 )
Diện tích toàn phần là:
$\frac{{272}}{{35}} + \frac{6}{7} \times 2 = \frac{{332}}{{35}}$ (dm 2 )