Bài 15. Phương trình tốc độ phản ứng và hằng số tốc độ phản ứng trang 63, 64, 65 SBT Hóa 10 Chân trời sáng tạo
Cho phương trình hoá học: 2KMnO4(aq) + 10FeSO4(aq) + 8H2SO4(aq) -> 5Fe2(SO4)3(aq) + K2SO4(aq) + 2MnSO4(aq) + 8H2O(l) Với cùng một lượng các chất tham gia phản ứng, chất phản ứng hết nhanh nhất là:
15.1
Cho phương trình hoá học:
2KMnO 4 (aq) + 10FeSO 4 (aq) + 8H 2 SO 4 (aq)
-> 5Fe 2 (SO 4 ) 3 (aq) + K 2 SO 4 (aq) + 2MnSO 4 (aq) + 8H 2 O(l)
Với cùng một lượng các chất tham gia phản ứng, chất phản ứng hết nhanh nhất là:
A. KMnO 4 .
B. FeSO 4 .
C. H 2 SO 4 .
D. Cả 3 chất hết cùng lúc.
Phương pháp giải:
So sánh hệ số của các chất tham gia, chất nào có hệ số càng lớn thì càng nhanh hết
Lời giải chi tiết:
- Đáp án: B
15.2
Đối với phản ứng: A + 3B → 2C, phát biểu nào sau đây đúng?
A. Tốc độ tiêu hao chất B bằng 3/2 tốc độ tạo thành chất C.
B. Tốc độ tiêu hao chất B bằng 2/3 tốc độ tạo thành chất C.
C. Tốc độ tiêu hao chất B bằng 3 tốc độ tạo thành chất C.
D. Tốc độ tiêu hao chất B bằng 1/3 tốc độ tạo thành chất C.
Phương pháp giải:
Dựa vào tỉ lệ mol hoặc hệ số của các chất trong phản ứng sẽ tỉ lệ với tốc độ tiêu hao/ tốc độ tạo thành của các chất
Lời giải chi tiết:
- Có 2.nB = 3.nC => \(\frac{{{n_B}}}{{{n_C}}} = \frac{3}{2}\) => Tốc độ tiêu hao chất B bằng 3/2 tốc độ tạo thành chất C
=> Đáp án: A
15.3
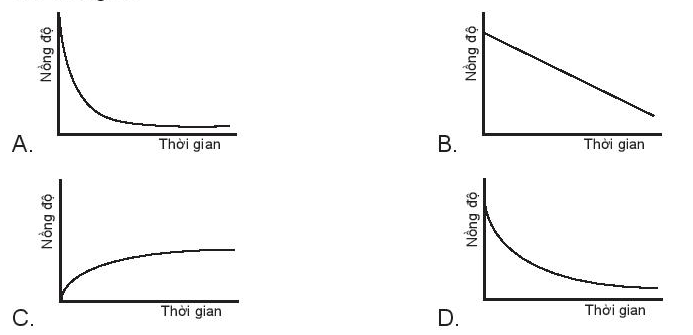
Biểu đồ nào sau đây không biểu diễn sự phụ thuộc nồng độ chất tham gia với thời gian
Phương pháp giải:
- Nồng độ chất tham gia giảm dần theo thời gian
- Nồng độ chất sản phẩm tăng dần theo thời gian
Lời giải chi tiết:
- Nồng độ chất tham gia giảm dần theo thời gian => Đồ thị C không biểu diễn phụ thuộc nồng độ chất tham gia với thời gian
15.4
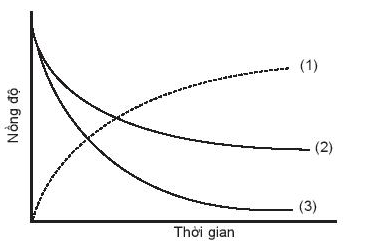
Đồ thị biểu diễn đường cong động học của phản ứng giữa oxygen và hydrogen tạo thành nước, O 2 (g) + 2H 2 (g) → 2H 2 O(g). Đường cong nào của hydrogen?
A. Đường cong số (1).
B. Đường cong số (2).
C. Đường cong số (3).
D. Đường cong số (2) hoặc (3) đều đúng.
Phương pháp giải:
Dựa vào
- Nồng độ chất tham gia giảm dần theo thời gian
- Nồng độ chất sản phẩm tăng dần theo thời gian
Lời giải chi tiết:
- Đáp án: C
15.5
Phương trình tổng hợp ammonia (NH 3 ), N 2 (g) + 3H 2 (g) → 2NH 3 (g). Nếu tốc độ tạo thành NH 3 là 0,345 M/s thì tốc độ của chất phản ứng H 2 là
A. 0,345 M/s.
B. 0,690 M/s.
C. 0,173 M/s.
D. 0,518 M/s.
Phương pháp giải:
Dựa vào tỉ lệ mol hoặc hệ số của các chất trong phản ứng sẽ tỉ lệ với tốc độ tiêu hao/ tốc độ tạo thành của các chất
Lời giải chi tiết:
- Có tỉ lệ: \(\frac{{{n_{{H_2}}}}}{{{n_{N{H_3}}}}} = \frac{{{V_{{H_2}}}}}{{{V_{N{H_3}}}}} = \frac{3}{2}\) => \({V_{{H_2}}} = \frac{{3.{V_{{N_2}}}}}{2} = \frac{{3.0,345}}{2} = 0,518M/s\) ð Đáp án: D
15.6
Phương trình hoá học của phản ứng: CHCl 3 (g) + Cl 2 (g) → CCl 4 (g) + HCl(g). Khi nồng độ của CHCl 3 giảm 4 lần, nồng độ Cl 2 giữ nguyên thì tốc độ phản ứng sẽ
A. tăng gấp đôi
B. giảm một nửa.
C. tăng 4 lần.
D. giảm 4 lần.
Phương pháp giải:
Dựa vào biểu thức tốc độ tức thời của phản ứng
aA + bB -> cC + dD là \(v = k.C_A^a.C_B^b\)
Lời giải chi tiết:
- Dựa theo biểu thức tốc độ tức thời ta có: \(v = k.C_{CHC{l_3}}^1.C_{C{l_2}}^1\)
- Khi giảm nồng độ CHCl 3 đi 4 lần ta có: \(v' = k.\frac{{C_{CHC{l_3}}^1}}{4}.C_{C{l_2}}^1\) => \(v' = \frac{v}{4}\)
=> Tốc độ phản ứng giảm 4 lần
=> Đáp án: D
15.7
Cho phương trình hoá học của phản ứng:
CO(g) + H 2 O(g) → CO 2 (g) + H 2 (g)
Viết biểu thức tốc độ của phản ứng trên. Khi nồng độ CO tăng 2 lần, lượng hơi nước không thay đổi, tốc độ phản ứng thay đổi như thế nào?
Phương pháp giải:
Dựa vào biểu thức tốc độ tức thời của phản ứng
aA + bB -> cC + dD là \(v = k.C_A^a.C_B^b\)
Lời giải chi tiết:
- Dựa theo biểu thức tốc độ tức thời ta có: \(v = k.C_{CO}^1.C_{{H_2}O}^1\)
- Khi nồng độ CO tăng 2 lần ta có: \(v' = k.{(2.C_{CO}^{})^1}.C_{{H_2}O}^1\) => \(v' = 2v\)
=> Tốc độ phản ứng tăng 2 lần
15.8
Từ dữ kiện trong Ví dụ 1 (SGK trang 95), tính tốc độ trung bình của phản ứng theo giá trị nồng độ của MgCl 2 trong 40 giây (bỏ qua sự thay đổi không đáng kể về thể tích dung dịch sau phản ứng). So sánh giá trị tốc độ phản ứng tính theo HCl với tính theo MgCl 2 .
Phương pháp giải:
aA + bB -> cC + dD là \(\overline v = - \frac{1}{a}.\frac{{\Delta {C_A}}}{{\Delta t}} = - \frac{1}{b}.\frac{{\Delta {C_B}}}{{\Delta t}} = \frac{1}{c}.\frac{{\Delta {C_C}}}{{\Delta t}} = \frac{1}{d}.\frac{{\Delta {C_D}}}{{\Delta t}}\)
Trong đó:
+ \(\overline v \): tốc độ trung bình của phản ứng
+ \(\Delta C = {C_2} - {C_1}\): sự biến thiên nồng độ
+ \(\Delta t = {t_2} - {t_1}\): sự biến thiên thời gian
Lời giải chi tiết:
- Có C M (HCl) = 0,8 - 0,6 = 0,2 M
- Theo phương trình: Mg(s) + 2HCl(aq) -> MgCl 2 (aq) + H 2 (g)
0,2 -> 0,1 (M)
- Tốc độ trung bình của phản ứng tính theo MgCl 2 trong 40s là:
\(\overline v = \frac{1}{1}.\frac{{0,1}}{{40}} = 2,{5.10^{ - 3}}\) (M/s)
=> Vậy giá trị tốc độ phản ứng tính theo HCl với tính theo MgCl 2 là bằng nhau.
15.9
Một số phản ứng diễn ra với số mol chất phản ứng cụ thể theo thời gian được thể hiện trong bảng dưới đây.
|
Phản ứng |
Lượng chất phản ứng (mol) |
Thời gian (s) |
Tốc độ phản ứng (mol/s) |
|
1 |
2 |
30 |
? |
|
2 |
5 |
120 |
? |
|
3 |
1 |
90 |
? |
|
4 |
3,2 |
90 |
? |
|
5 |
5,9 |
30 |
? |
a) Tính tốc độ trung bình của mỗi phản ứng
b) Phản ứng nào diễn ra với tốc độ nhanh nhất? Phản ứng nào diễn ra với tốc độ chậm nhất?
Phương pháp giải:
Dựa vào biểu thức tốc độ trung bình của phản ứng:
aA + bB -> cC + dD là \(\overline v = - \frac{1}{a}.\frac{{\Delta {C_A}}}{{\Delta t}} = - \frac{1}{b}.\frac{{\Delta {C_B}}}{{\Delta t}} = \frac{1}{c}.\frac{{\Delta {C_C}}}{{\Delta t}} = \frac{1}{d}.\frac{{\Delta {C_D}}}{{\Delta t}}\)
+ \(\overline v \): tốc độ trung bình của phản ứng
+ \(\Delta C = {C_2} - {C_1}\): sự biến thiên nồng độ
+ \(\Delta t = {t_2} - {t_1}\): sự biến thiên thời gian
Lời giải chi tiết:
a) Tốc độ trung bình của mỗi phản ứng là:
|
Phản ứng |
Lượng chất phản ứng (mol) |
Thời gian (s) |
Tốc độ phản ứng (mol/s) |
|
1 |
2 |
30 |
0,06667 |
|
2 |
5 |
120 |
0,04167 |
|
3 |
1 |
90 |
0,01111 |
|
4 |
3,2 |
90 |
0,03556 |
|
5 |
5,9 |
30 |
0,19667 |
b) Phản ứng 5 diễn ra với tốc độ nhanh nhất, phản ứng 3 diễn ra với tốc độ chậm nhất
15.10
Hai phương trình hoá học của phản ứng xảy ra với cùng một lượng Cl 2 như sau:
Mg(s) + Cl 2 (g) → MgCl 2 (s) (1)
2Na(s) + Cl 2 (g) → 2NaCl(s) (2)
Sau 1 phút, khối lượng MgCl 2 được tạo ra 2 gam.
a) Tính tốc độ trung bình (mol/s) của phản ứng (1).
b) Nếu tốc độ trung bình xảy ra trong phản ứng (2) tương đương (1), thì khối lượng sản phẩm NaCl thu được là bao nhiêu?
Phương pháp giải:
Dựa vào biểu thức tốc độ trung bình của phản ứng:
aA + bB -> cC + dD là \(\overline v = \frac{n}{{\Delta t}}\)
+ \(\overline v \): tốc độ trung bình của phản ứng
+ n: số mol chất phản ứng
+ \(\Delta t = {t_2} - {t_1}\): sự biến thiên thời gian
Lời giải chi tiết:
a) - \({n_{MgC{l_2}}} = \frac{2}{{95}}\)mol
- Tốc độ trung bình (mol/s) của phản ứng (1) là \(\overline v = \frac{2}{{95.60}} = 3,{5.10^{ - 4}}\)
b) \({m_{NaCl}} = 3,{5.10^{ - 4}}.58,5 = 0,02\)(gam/s)
15.11
Cho phản ứng tert-butyl chloride (tert–C 4 H 9 Cl) với nước:
C 4 H 9 Cl(l) + H 2 O(l) → C 4 H 9 OH(aq) + HCl(aq)
Tính tốc độ trung bình của phản ứng theo tert–butyl chloride, với nồng độ ban đầu là 0,22 M, sau 4s, nồng độ còn lại 0,10 M.
Phương pháp giải:
Dựa vào biểu thức tốc độ trung bình của phản ứng:
aA + bB -> cC + dD là \(\overline v = - \frac{1}{a}.\frac{{\Delta {C_A}}}{{\Delta t}} = - \frac{1}{b}.\frac{{\Delta {C_B}}}{{\Delta t}} = \frac{1}{c}.\frac{{\Delta {C_C}}}{{\Delta t}} = \frac{1}{d}.\frac{{\Delta {C_D}}}{{\Delta t}}\)
+ \(\overline v \): tốc độ trung bình của phản ứng
+ \(\Delta C = {C_2} - {C_1}\): sự biến thiên nồng độ
+ \(\Delta t = {t_2} - {t_1}\): sự biến thiên thời gian
Lời giải chi tiết:
- Tốc độ trung bình của phản ứng là: \(\overline v = \frac{{0,22 - 0,10}}{4} = 0,03\)(mol/s)
15.12
Xét phản ứng hoá học đơn giản giữa hai chất A và B theo phương trình: A + B → C. Từ thông tin đã cho, hoàn thành bảng dưới đây:
|
Thực nghiệm |
Nồng độ chất A (M) |
Nồng độ chất B (M) |
Tốc độ phản ứng (M/s) |
|
1 |
0,20 |
0,050 |
0,24 |
|
2 |
? |
0,030 |
0,20 |
|
3 |
0,40 |
? |
0,80 |
Phương pháp giải:
Dựa vào biểu thức tốc độ tức thời của phản ứng
aA + bB -> cC + dD là \(v = k.C_A^a.C_B^b\)
Lời giải chi tiết:
- Từ thực nghiệm 1 ta có: k = \(\frac{v}{{{C_A}.{C_B}}} = \frac{{0,24}}{{0,2.0,05}} = 24\)
- Từ đó ta tính được:
+ Trong thực nghiệm 2:
C A = \(\frac{v}{{k.{C_B}}} = \frac{{0,20}}{{24.0,03}} = 0,278M\)
+ Trong thực nghiệm 3:
C B = \(\frac{v}{{k.{C_A}}} = \frac{{0,80}}{{24.0,40}} = 0,083M\)
|
Thực nghiệm |
Nồng độ chất A (M) |
Nồng độ chất B (M) |
Tốc độ phản ứng (M/s) |
|
1 |
0,20 |
0,050 |
0,24 |
|
2 |
0,278 |
0,030 |
0,20 |
|
3 |
0,40 |
0,083 |
0,80 |
15.13
Xét phản ứng phân huỷ khí N 2 O 5 xảy ra như sau:
2N 2 O 5 (g) → 4NO 2 (g) + O 2 (g)
a) Viết biểu thức tính tốc độ phản ứng theo sự biến thiên nồng độ của chất tham gia và sản phẩm theo thời gian.
b) Sau khoảng thời gian t (s), tốc độ tạo thành O 2 là 9,0 × 10 -6 (M/s), tính tốc độ của các chất còn lại trong phản ứng.
Phương pháp giải:
- Biểu thức tốc độ trung bình của phản ứng:
aA + bB -> cC + dD là \(\overline v = - \frac{1}{a}.\frac{{\Delta {C_A}}}{{\Delta t}} = - \frac{1}{b}.\frac{{\Delta {C_B}}}{{\Delta t}} = \frac{1}{c}.\frac{{\Delta {C_C}}}{{\Delta t}} = \frac{1}{d}.\frac{{\Delta {C_D}}}{{\Delta t}}\)
+ \(\overline v \): tốc độ trung bình của phản ứng
+ \(\Delta C = {C_2} - {C_1}\): sự biến thiên nồng độ
+ \(\Delta t = {t_2} - {t_1}\): sự biến thiên thời gian
- Biểu thức tốc độ tức thời của phản ứng aA + bB " cC + dD là \(v = k.C_A^a.C_B^b\)
Lời giải chi tiết:
a) Biểu thức tốc độ trung bình của phản ứng là:
\(\overline v = - \frac{1}{2}.\frac{{\Delta {C_{{N_2}{O_5}}}}}{{\Delta t}} = \frac{1}{1}.\frac{{\Delta {C_{{O_2}}}}}{{\Delta t}} = \frac{1}{4}.\frac{{\Delta {C_{N{O_2}}}}}{{\Delta t}}\)
b) Từ hệ số cân bằng của phương trình ta có:
+ Tốc độ tạo thành NO 2 là \({v_{N{O_2}}} = 4{v_{{O_2}}} = 4.9,{0.10^{ - 6}} = 3,{6.10^{ - 5}}\) (M/s)
+ Tốc độ tạo thành N 2 O 5 là \({v_{{N_2}{O_5}}} = 2{v_{{O_2}}} = 2.9,{0.10^{ - 6}} = 1,{8.10^{ - 5}}\) (M/s)
15.14
Sulfuric acid (H 2 SO 4 ) là hoá chất quan trọng trong công nghiệp, ứng dụng trong sản xuất phân bón, lọc dầu, xử lí nước thải,... Một giai đoạn để sản xuất H 2 SO 4 là phản ứng 2SO 2 (g) + O 2 (g) → 2SO 3 (g), kết quả thực nghiệm của phản ứng cho giá trị theo bảng:
|
Thời gian (s) |
SO 2 (M) |
O 2 (M) |
SO 3 (M) |
|
300 |
0,0270 |
0,0500 |
0,0072 |
|
720 |
0,0194 |
0,0462 |
0,0148 |
Tính tốc độ trung bình của phản ứng trong khoảng thời gian trên
Phương pháp giải:
aA + bB -> cC + dD là \(\overline v = - \frac{1}{a}.\frac{{\Delta {C_A}}}{{\Delta t}} = - \frac{1}{b}.\frac{{\Delta {C_B}}}{{\Delta t}} = \frac{1}{c}.\frac{{\Delta {C_C}}}{{\Delta t}} = \frac{1}{d}.\frac{{\Delta {C_D}}}{{\Delta t}}\)
+ \(\overline v \): tốc độ trung bình của phản ứng
+ \(\Delta C = {C_2} - {C_1}\): sự biến thiên nồng độ
+ \(\Delta t = {t_2} - {t_1}\): sự biến thiên thời gian
Lời giải chi tiết:
- Từ bảng số liệu ta có:
+ \(\Delta t = {t_2} - {t_1} = 720 - 300 = 420\)s
+ \(\Delta {C_{S{O_2}}} = 0,0194 - 0,0270 = - 7,{6.10^{ - 3}}\)M
+ \(\Delta {C_{{O_2}}} = 0,0462 - 0,0500 = - 3,{8.10^{ - 3}}\)M
+ \(\Delta {C_{S{O_2}}} = 0,0148 - 0,0072 = 7,{6.10^{ - 3}}\)M
- Tốc độ trung bình của phản ứng là:
\(\overline v = - \frac{1}{2}.\frac{{\Delta {C_{S{O_2}}}}}{{\Delta t}} = - \frac{1}{1}.\frac{{\Delta {C_{{O_2}}}}}{{\Delta t}} = \frac{1}{2}.\frac{{\Delta {C_{S{O_3}}}}}{{\Delta t}} = {9.10^{ - 6}}\) (M/s)