Bài 27. Hiệu suất trang 50, 51 SBT Vật lí 10 Kết nối tri thức với cuộc sống
Hiệu suất là tỉ số giữa
27.1
Hiệu suất là tỉ số giữa
A. năng lượng hao phí và năng lượng có ích.
B. năng lượng có ích và năng lượng hao phí.
C. năng lượng hao phí và năng lượng toàn phần.
D. năng lượng có ích và năng lượng toàn phần.
Phương pháp giải:
Nắm được khái niệm về hiệu suất.
Lời giải chi tiết:
Để đánh giá tỉ lệ giữa năng lượng có ích và năng lượng toàn phần, người ta dùng khái niệm hiệu suất.
H = \(\frac{{{{\rm{W}}_i}}}{{{{\rm{W}}_{tp}}}}.100\% \) hay H = \(\frac{{{P_i}}}{{{P_{tp}}}}.100\% \).
Trong đó:
+ W i : Năng lượng có ích.
+ W tp : Năng lượng toàn phần.
+ P i : Công suất có ích.
+ P tp : Công suất toàn phần.
Chọn đáp án D.
27.2
Hiệu suất càng cao thì
A. tỉ lệ năng lượng hao phí so với năng lượng toàn phần càng lớn.
B. năng lượng tiêu thụ càng lớn.
C. năng lượng hao phí càng ít.
D. tỉ lệ năng lượng hao phí so với năng lượng toàn phần càng ít.
Phương pháp giải:
Vận dụng công thức tính hiệu suất để giải thích:
H = \(\frac{{{{\rm{W}}_i}}}{{{{\rm{W}}_{tp}}}}.100\% \)
Trong đó:
+ W i : Năng lượng có ích.
+ W tp : Năng lượng toàn phần.
Lời giải chi tiết:
Từ công thức tính hiệu suất: H = \(\frac{{{{\rm{W}}_i}}}{{{{\rm{W}}_{tp}}}}.100\% \)
Trong đó:
+ W i : Năng lượng có ích.
+ W tp : Năng lượng toàn phần.
è Hiệu suất tỉ lệ thuận với phần năng lượng có ích đã tiêu thụ và tỉ lệ nghịch với năng lượng toàn phần. Vì vậy hiệu suất càng lớn thì phần năng lượng có ích đã tiêu thụ càng lớn và tỉ lệ năng lượng hao phí so với năng lượng toàn phần càng ít.
Chọn đáp án D.
27.3
Một công nhân xây dựng sử dụng ròng rọc để kéo một thùng sơn nặng 27 kg lên dàn giáo cao 3,1 m so với mặt đất (Hình 27.1). Lực mà người công nhân kéo theo phương thẳng đứng có độ lớn 310 N. Lấy g = 9,8 m/s 2 .

a) Tính công mà người thợ đã thực hiện.
b) Tính phần công có ích dùng để kéo thùng sơn.
c) Tính hiệu suất của quá trình này.
Phương pháp giải:
a) Áp dụng công thức tính công: A = F.s.
b) Phần công có ích dùng để kéo thùng sơn chính là công đã dùng để chiến thắng trọng lực: A có ích = P.s = m.g.s.
c) Áp dụng công thức tính hiệu suất: H = \(\frac{{{A_i}}}{{{A_{tp}}}}.100\% \).
Lời giải chi tiết:
a) Công mà người thợ đã thực hiện là: A = F.s = 310.3,1 = 961 J.
b) Phần công có ích dùng để kéo thùng sơn là:
A có ích = P.s = m.g.s = 27.9,8.3,1 = 820,26 J.
c) Hiệu suất của quá trình này là:
Áp dụng công thức tính hiệu suất ta có: H = \(\frac{{{A_i}}}{{{A_{tp}}}}.100\% \)= \(\frac{{820,26}}{{961}}.100\% \)≈ 85,4 %.
27.4
Một quả bóng có khối lượng 200 g được ném thẳng đứng lên cao với vận tốc ban đầu là 15 m/s. Nó đạt được độ cao 10 m so với vị trí ném. Lấy g = 9,8 m/s 2 , tính tỉ lệ cơ năng của vật đã bị biến đổi do lực cản của không khí.
Phương pháp giải:
Chọn mốc thế năng ở vị trí ném.
Tính cơ năng của quả bóng lúc đầu và lúc sau.
Trong đó:
W = W đ + W t = \(\frac{1}{2}mv_0^2\) + mgh.
Tỉ lệ cơ năng bị biến đổi do lực cản: \(\frac{{{{\rm{W}}_s} - {{\rm{W}}_d}}}{{{{\rm{W}}_d}}}.100\% \)
Lời giải chi tiết:
Chọn mốc thế năng ở vị trí ném.
Cơ năng ban đầu: W 1 = \(\frac{1}{2}mv_0^2\) = \(\frac{1}{2}.0,{2.15^2}\) = 22,5 J.
Cơ năng lúc sau: W 2 = mgh = 0,2.10.10 = 20 J.
Tỉ lệ cơ năng bị biến đổi do lực cản: \(\frac{{{{\rm{W}}_2} - {{\rm{W}}_1}}}{{{{\rm{W}}_1}}}.100\% \) ≈ 11,1%.
27.5
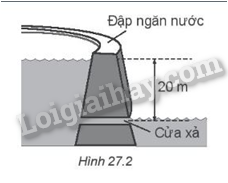
Mực nước bên trong đập ngăn nước của một nhà máy thuỷ điện có độ cao 20 m so với cửa xả với tốc độ 16 m/s. Tính tỉ lệ phần thể năng của nước đã được chuyên hoá thành động năng.
Phương pháp giải:
Xét với cùng một lượng nước không đổi (khối lượng m).
Chọn mốc thế năng tại cửa xả.
\(\frac{{{{\rm{W}}_d}}}{{{{\rm{W}}_t}}}.100\% = \frac{{0,5.m{v^2}}}{{mgh}}.100\% .\)Tỉ lệ phần thế năng chuyển hóa thành động năng
Lời giải chi tiết:
Xét với cùng một lượng nước không đổi (khối lượng m).
Chọn mốc thế năng tại cửa xả.
Thế năng của nước ở độ cao 20 m: W t = mgh.
Động năng của nước ở cửa xả: W đ = \(\frac{1}{2}m{v^2}\).
Tỉ lệ phần thế năng chuyển hóa thành động năng: \(\frac{{{{\rm{W}}_d}}}{{{{\rm{W}}_t}}}.100\% = \frac{{0,5.m{v^2}}}{{mgh}}.100\% = \frac{{0,{{5.16}^2}}}{{9,8.20}} \approx 65,3\% .\)
27.6
Một vận động viên nhảy dù có khối lượng 70 kg thực hiện động tác nhảy dù từ độ cao 500 m so với mặt đất. Sau một đoạn đường rơi tự do thị vận động viên bật dù và tiếp đất với vận tốc 8 m/s. Lấy g = 9,8 m/s 2 .
a) Tính thế năng của vận động viên so với mặt đất trước khi nhảy dù.
b) Tính động năng của vận động viên khi tiếp đất.
c) Tính công của lực cản của không khí.
Phương pháp giải:
a) Áp dụng công thức tính thế năng: W t = mgh.
b) Áp dụng công thức tính động năng: W đ = \(\frac{1}{2}m{v^2}\).
c) A cản = W sau - W đầu .
Lời giải chi tiết:
Chọn mốc thế năng ở mặt đất.
a) Thế năng của vận động viên so với mặt đất trước khi nhảy dù là:
W t = mgh = 70.9,8.500 = 343 000 J.
b) Động năng của vận động viên khi tiếp đất là:
W đ = \(\frac{1}{2}m{v^2}\)= \(\frac{1}{2}{70.8^2}\) = 2 240 J.
c) Ta có:
Cơ năng của vận động viên trước khi nhảy dù là: W đầu = W t = 343 000 J.
Cơ năng của vận động viên khi tiếp đất là: W sau = W đ = 2 240 J.
Công của lực cản của không khí là:
A cản = W sau - W đầu = 2240 – 343000 = - 340760 J.
27.7
Một tàu lượn siêu tốc có điểm cao nhất cách điểm thấp nhất 94,5m theo phương thẳng đứng. Tàu lượn được thả không vận tốc ban đầu từ điểm cao nhất. a) Tìm vận tốc cực đại mà tàu lượn có thể đạt được.
b) Trên thực tế, vận tốc cực đại của tàu lượn đạt được là 41,1 m/s. Tính hiệu suất của quá trình chuyển đổi thế năng thành động năng của tàu lượn.
Phương pháp giải:
a) Tàu lượn đạt vận tốc cực đại khi ở điểm thấp nhất đồng thời không có sự hao phí năng lượng khi tàu chuyển động: W 2 = W 1 .
b) Áp dụng công thức tính hiệu suất: H = \(\frac{{{\rm{W}}_d^'}}{{{{\rm{W}}_d}}}.100\% \).
Lời giải chi tiết:
Chọn mốc thế năng ở điểm thấp nhất mà tàu lượn đạt tới.
Cơ năng của tàu lượn ở điểm cao nhất: W 1 = W t = mgh.
Cơ năng của tàu lượn ở điểm thấp nhất: W 2 = W đ = \(\frac{1}{2}m{v^2}\).
a) Tàu lượn đạt vận tốc cực đại khi ở điểm thấp nhất đồng thời không có sự hao phí năng lượng khi tàu chuyển động: W 2 = W 1 .
ó \(\frac{1}{2}m{v^2}\)= mgh è v = \(\sqrt {2gh} \)= \(\sqrt {2.9,8.94,5} \)≈ 43,04 m/s.
b) Hiệu suất của quá rính chuyển đổi là:
H = \(\frac{{{\rm{W}}_d^'}}{{{{\rm{W}}_d}}}.100\% \) = \(\frac{{0,5.m.v_2^'}}{{0,5.m.{v^2}}}.100\% \) = \(\frac{{41,{1^2}}}{{43,{{04}^2}}}.100\% \) ≈ 91,2 %.
27.8
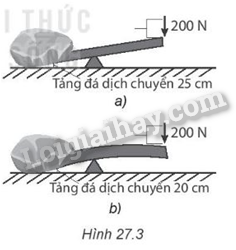
Một người sử dụng đòn bẩy để nâng một tảng đá trọng lượng 600 N lên bằng cách tác dụng một lực 200 N vào một đầu đòn bẩy làm cho đầu đòn bẩy này dịch chuyển 80 cm (Hình 27.3a).
a) Tảng đá dịch chuyển một đoạn 25 cm. Tính hiệu suất của đòn bẩy.
b) Trên thực tế, đòn bẩy không tuyệt đối cũng nên nó bị cong và tảng đá chỉ dịch chuyển 20 cm (Hình 27.3b). Tính hiệu suất của đòn bẩy.
Phương pháp giải:
Áp dụng công thức tính hiệu suất: H = \(\frac{{{A_i}}}{{{A_{tp}}}}.100\% \).
Trong đó: A = F.s.
Lời giải chi tiết:
a) Hiệu suất của đòn bẩy trong trường hợp tảng đá dịch chuyển một đoạn 25 cm = 0,25 m là:
H 1 = \(\frac{{{A_i}}}{{{A_{tp}}}}.100\% \) = \(\frac{{600.0,25}}{{200.0,8}}.100\% \) = 93,75 %.
a) Hiệu suất của đòn bẩy trong trường hợp tảng đá dịch chuyển một đoạn 20 cm = 0,2 m là:
H 1 = \(\frac{{{A_i}}}{{{A_{tp}}}}.100\% \) = \(\frac{{600.0,2}}{{200.0,8}}.100\% \) = 75 %.