Ôn tập chương III trang 40, 41, 42 SBT Vật lí 10 Kết nối tri thức với cuộc sống
Chọn câu đúng.
III.1
Chọn câu đúng.
A. Nếu không chịu lực nào tác dụng thì mọi vật phải đứng yên.
B. Vật chuyển động được là nhờ có lực tác dụng lên nó.
C. Khi không còn lực nào tác dụng lên vật nữa, thì vật đang chuyển động sẽ
lập tức dừng lại.
D. Khi thấy vận tốc của vật thay đổi thì chắc chắn là đã có lực tác dụng lên vật.
Phương pháp giải:
Vận dụng định luật I Newton.
Lời giải chi tiết:
A sai vì nếu không chịu lực nào tác dụng thì vật đang đứng yên sẽ tiếp tục đứng yên, vật đang chuyển động sẽ tiếp tục chuyển động thẳng đều.
B sai vì khi vật đang chuyển động nếu không có lực nào tác dụng lên nó thì nó sẽ vẫn tiếp tục chuyển động thẳng đều.
C sai vì khi không còn lực nào tác dụng lên vật nữa thì vật đang chuyển động sẽ tiếp tục chuyển động thẳng đều.
D đúng khi có lực tác dụng lên vật thì gia tốc sẽ thay đổi dẫn đến vận tốc cũng sẽ thay đổi.
Chọn đáp án D.
III.2
Cách viết hệ thức của định luật 2 Newton nào dưới đây là đúng?
A. \(\overrightarrow F \) = \(ma\).
B. \(\overrightarrow F \) = \(m\overrightarrow a \).
C. -\(\overrightarrow F \) = \(m\overrightarrow a \).
D. \(\overrightarrow F \) = \( - m\overrightarrow a \).
Phương pháp giải:
Theo định luật II Newton: \(\overrightarrow F \) = \(m\overrightarrow a \).
Lời giải chi tiết:
Theo định luật II Newton: \(\overrightarrow F \) = \(m\overrightarrow a \).
Chọn đáp án B.
III.3
Cho hai lực khác phương, có độ lớn bằng 9 N và 12 N. Độ lớn của hợp lực
Có thể nhận giá trị nào sau đây?
A. 15 N. B. 1 N. C. 2N. D. 25 N.
Phương pháp giải:
Sử dụng công thức: |F1 – F2| ≤ F ≤ F1 + F2
Lời giải chi tiết:
Ta luôn có: |F1 – F2| ≤ F ≤ F1 + F2 => 3 N ≤ F ≤ 21 N.
=> Hợp lực của hai lực này có thể có độ lớn là 15 N.
Chọn đáp án A.
III.4
Chất điểm chịu tác dụng của lực có độ lớn là F 1 và F 2 = 6 N. Biết hai lực này hợp với nhau góc 150° và hợp lực của chúng có giá trị nhỏ nhất. Giá trị của F 1 là
A. 2N. B. 3\(\sqrt 3 \) N. C.3 N. D. 5 N
Phương pháp giải:
Áp dụng công thức tính độ lớn của lực tổng hợp trong trường hợp tổng quát:
\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}cos\varphi } \)
(φ: góc hợp giữa hai lực thành phần)
Lời giải chi tiết:
Ta có: \({F^2} = F_1^2 + F_2^2 + 2{F_1}{F_2}\cos {150^o}\) ó \(F_1^2 - 6\sqrt 3 {F_1} + 36 - {F^2} = 0\) (*)
(*) là phương trình bậc 2 đối với F 1 có \(\Delta = {\left( {6\sqrt 3 } \right)^2} - 4(32 - {F^2}).\)
Để phương trình có nghiệm thì:
∆ ≥ 0 ó \({\left( {6\sqrt 3 } \right)^2} - 4(32 - {F^2})\) ≥ 0 => F min = \(\sqrt 5 \) N.
Dấu “=” xảy ra khi F 1 = 3\(\sqrt 3 \) N.
Chọn đáp án B
III.5
Một ô tô có khối lượng 800 kg có thể đạt được tốc độ 18 m/s trong 36 s kể từ lúc khởi hành. Lấy g = 10 m/s 2 .
a) Lực để gây ra gia tốc cho xe có độ lớn bằng bao nhiêu?
b) Tính tỉ số độ lớn của lực tăng tốc và trọng lượng của xe.
Phương pháp giải:
a) Tính gia tốc của xe bằng công thức: a = \(\frac{{v - {v_0}}}{t}\)
Áp dụng định luật II Newton, có: F = ma.
b) Lực tăng tốc chính là lực gây ra tốc cho xe đã tính ở câu a)
Tính trọng lượng của xe bằng công thức: P = mg.
=> Tính tỉ số: \(\frac{F}{P}\).
Lời giải chi tiết:
a) a = \(\frac{{v - {v_0}}}{t}\)=\(\frac{{18 - 0}}{{36}}\)= - 0,5 m/s 2 .
Lực cần thiết để gây ra gia tốc cho ô tô là hợp lực cùng chiều với gia tốc có độ lớn: F = ma = 800.0,5 = 400 N.
b) \(\frac{F}{P} = \frac{{400}}{{800.10}}\)=\(\frac{1}{{20}}.\)
III.6
An và Bình cùng nhau đẩy một thùng hàng chuyền động thẳng trên sàn nhà. Thùng hàng có khối lượng 120 kg. An đẩy với một lực 450 N, Bình đẩy với một lực 350 N cùng theo phương ngang. Hệ số ma sát trượt giữa thùng và sàn là 0,2. Tính gia tốc của thùng, lấy g = 10 m/s 2 .
Phương pháp giải:
Tính lực ma sát tác dụng lên thùng hàng: F ma sát = μmg.
Áp dụng định luật II Newton có: F = F đẩy – F ma sát = ma => a.
Lời giải chi tiết:
Hợp lực tác dụng lên thùng hàng: F = F đẩy – F ma sát , với F ma sát = μmg = 240 N.
=> F = 800 – 240 = 560 N => a = \(\frac{F}{m}\)= \(\frac{{560}}{{120}}\)= 4,67 m/s 2 .
III.7
Một xe ô tô có khối lượng 1,2 tấn tắt máy và hãm phanh. Xe chuyển động chậm dần đều cho đến khi dừng lại thì đi được quãng đường 96 m. Biết quãng đường xe đi được trong giây đầu tiên gấp 15 lần quãng đường xe đi được trong giây cuối. Xác định độ lớn của hợp lực tác dụng vào xe trong quá trình chuyển động chậm dần đều.
Phương pháp giải:
Vận dụng phương trình của chuyển động s = v 0 t + \(\frac{1}{2}a{t^2}\) để đi tìm gia tốc a.
Theo định luật II Newton, độ lớn của hợp lực F = ma.
Lời giải chi tiết:
Gọi t là thời gian từ lúc xe hãm phanh tới khi dừng hẳn, v 0 là tốc độ tại thời điểm xe hãm phanh.
Quãng đường xe đi được trong giây đầu tiên: s đầu = v 0 t 1 + \(\frac{1}{2}at_1^2\)
s đầu = v 0 t 1 + \(\frac{1}{2}at_1^2\) = v 0 + 0,5a (với t 1 = 1 s).
Quãng đường xe đi được trong giây cuối cùng:
s cuối = s t – s t-1 = v 0 t+ \(\frac{1}{2}a{t^2}\)- (v 0 (t-1) + \(\frac{1}{2}\)a(t-1) 2 ) = v 0 + at – 0,5a
Vật chuyển động chậm dần dều đến khi dừng lại v = 0, nên ta có: v 0 + at = 0 (1)
Suy ra: s cuối = -0,5a
Theo giả thiết: = \(\frac{{{v_0} + 0,5a}}{{ - 0,5a}} = 15\)=> v 0 = -8a (2)
Từ (1) và (2) => t = 8 s.
Lại có: s = v 0 t+ \(\frac{1}{2}a{t^2}\)ó 96 = -32a => a = -3 m/s 2 .
=> Lực hãm tác dụng vào xe là: F = |ma| = |1200.(-3)| = 3600 N.
III.8
Một người nhảy dù có khối lượng tổng cộng 100 kg. Trong thời gian đầu (khoảng vài giây) kể từ khi bắt đầu nhảy xuống, người này chưa mở dù và rơi dưới tác dụng của trọng lực. Khi người đó mở dù, lực tác dụng của dù lên người là 2 000 N hướng lên.
a) Biểu diễn các lực tác dụng lên người nhảy dù khi mở dù.
b) Xác định hợp lực tác dụng lên người nhảy dù khi mở dù.
c) Người sẽ chuyển động như thế nào kể từ khi mở dù?
Phương pháp giải:
b) Vận dụng biểu thức véc-tơ lực tổng hợp sau: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \).
Tính trọng lượng của người nhảy dù: P = mg.
c) Áp dụng định luật II Newton: F = ma => a.
Lời giải chi tiết:
Trọng lượng tổng cộng của người nhảy dù: P = 1000 N.
a) Các lực tác dụng lên người nhảy dù khi mở dù được biểu diễn như hình vẽ.
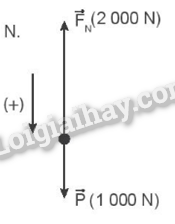
b) Chọn chiều (+) thẳng đứng hướng lên.
Theo quy tắc tổng hợp lực ta có:
F = F N – P = 2000 – 1000 = 1000 N.
Vậy hợp lực tác dụng lên người nhảy dù hướng lên và có độ lớn F = 1000 N.
c) Khi chưa mở dù, người nhảy dù chuyển động nhanh dần đều dưới tác dụng của trọng lực (rơi tự do). Sau khi mở dù, người nhảy dù sẽ chuyển động chậm dần đều với gia tốc: a = \(\frac{{ - F}}{m}\)= \(\frac{{ - 1000}}{{100}}\)= -10 m/s 2 .
III.9
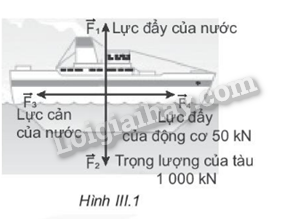
Con tàu trong Hình III.1 đang chuyển động theo một hướng xác định với vận tốc không đổi.
a) Tại sao nói con tàu đang ở trạng thái cân bằng (hợp lực bằng 0)?
b) Xác định lực đẩy \(\overrightarrow {{F_1}} \) của nước.
c) Xác định lực cản \(\overrightarrow {{F_3}} \) của nước.
Phương pháp giải:
a) Áp dụng định luật II Newton để giải thích.
b) c) Áp dụng định luật III Newton để giải thích.
Lời giải chi tiết:
a) Theo định luật II Newton:
Vì con tàu chuyển động theo một hướng xác định với vận tốc không đổi nên gia tốc của tàu a = 0. Do đó, tàu ở trạng thái cân bằng và hợp lực tác dụng F = 0.
b) Theo định luật III Newton thì lực đẩy \(\overrightarrow {{F_1}} \) của nước và trọng lượng \(\overrightarrow {{F_2}} \)của tàu là 2 lực trực đối nên F 1 = F 2 = 1000 kN.
c) Theo định luật III Newton thì lực cản \(\overrightarrow {{F_3}} \) của nước và lực đẩy \(\overrightarrow {{F_4}} \) của động cơ là 2 lực trực đối nên F 3 = F 4 = 50 kN.
III.10
Một vật khối lượng 2,5 kg đang nằm yên trên mặt phẳng ngang thì chịu tác dụng của lực kéo 15 N theo phương ngang và bắt đầu chuyển động. Biết trong 1 phút đầu tiên sau khi chịu tác dụng lực, vật đi được 2700 m. Coi lực cản tác dụng vào vật không đổi trong quá trình chuyển động. Xác định độ lớn của lực cản tác dụng vào vật.
Phương pháp giải:
Áp dụng công thức: s = v 0 t + \(\frac{1}{2}a{t^2}\)
Áp dụng định luật II Newton ta có: F k – F C = ma
Lời giải chi tiết:
Áp dụng công thức: s = v 0 t + \(\frac{1}{2}a{t^2}\)
Vì ban đầu vật đang đứng yên nên v 0 = 0 => s = \(\frac{1}{2}a{t^2}\)
=> a = \(\frac{{2s}}{{{t^2}}}\)= \(\frac{{2.2700}}{{{{60}^2}}}\)= 1,5 m/s 2
Áp dụng định luật II Newton ta có: F k – F C = ma
ó F C = F k – ma = 15 – 2,5.1,5 = 11,25 N.
III.11
Một thanh AB khối lượng 8 kg, dài 60 cm được treo nằm ngang nhờ hai sợi dây dài 50 cm như ở Hình III.2. Hai điểm treo cách nhau 120 cm. Lấy g = 10 m/s 2 . Xác định lực căng dây và lực kéo thanh.
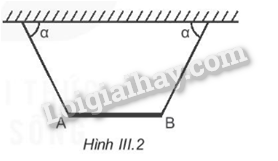
Phương pháp giải:
Viết phương trình cân bằng lực của thanh AB: \(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} + \overrightarrow P = \overrightarrow 0 \).
Chiều lên 2 trục thẳng đứng và nằm ngang.
Lời giải chi tiết:

Thanh AB chịu các lực như hình vẽ.
TA tính được: sinα = \(\frac{4}{5}\); P = 80N
Áp dụng điều kiện cân bằng của thanh:
\(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} + \overrightarrow P = \overrightarrow 0 \)
Chiếu lên hai trục thẳng đứng và nằm ngang.
Ta có:
T 1 = T 2 = \(\frac{P}{{2\sin \theta }}\)= 50 N
N = T 1 cosθ = 50.\(\frac{3}{5}\)= 30 N.
III.12
Dưới tác dụng của lực \(\overrightarrow F \) (Hình III.3), thanh AB có thể quay quanh điểm A. Xác định cánh tay đòn của lực \(\overrightarrow F \) trong trường hợp này (biết AB = 5 cm).
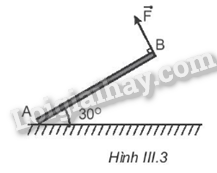
Phương pháp giải:
Cánh tay đòn của lực là khoảng cách từ giá của lực đến trục quay.
Lời giải chi tiết:
Cánh tay đòn của lực là khoảng cách từ giá của lực đến trục quay.
Do đó cánh tay đòn của lực F là AB = 5 cm.
III.13
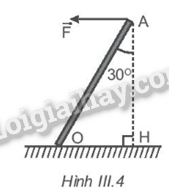
Tính moment của lực \(\overrightarrow F \) đối với trục quay O, cho biết F = 100 N, OA = 100 cm. Bỏ qua trong lượng của thanh (Hình III.4).
Phương pháp giải:
Áp dụng biểu thức tính moment lực: M = F.d.
Trong đó:
F: độ lớn của lực.
d: khoảng cách từ trục quay đến giá của lực.
Lời giải chi tiết:
Đổi OA = 100 cm = 1 m. Vì tam giác OAH vuông nên ta có OH = OA.cos30 o .
Áp dụng biểu thức tính moment lực:
M = F.d ó M = F.AH = 100.1.cos30 o =\(50\sqrt 3 \) N.m.
III.14
Hai lực của ngẫu lực có độ lớn F = 20 N, khoảng cách giữa hai giá của ngẫu lực là d = 30 cm, Xác định moment của ngẫu lực.
Phương pháp giải:
Áp dụng biểu thức tính moment của ngẫu lực: M = Fd.
Trong đó:
F: độ lớn của lực.
d: khoảng cách giữa giá của 2 lực.
Lời giải chi tiết:
Đổi d = 30 cm = 0,3 m.
Áp dụng biểu thức tính moment của ngẫu lực: M = F.d = 20.0,3 = 6 N.m.
III.15
Một vật rắn phẳng, mỏng có dạng một tam giác đều ABC, cạnh a = 20 cm. Người ta tác dụng một ngẫu lực nằm trong mặt phẳng của tam giác. Các lực này có độ lớn 8 N và đặt vào hai đỉnh A và C và song song với BC. Xác định moment của ngẫu lực.
Phương pháp giải:
Áp dụng biểu thức tính moment của ngẫu lực: M = Fd.
Trong đó:
F: độ lớn của lực.
d: khoảng cách giữa giá của 2 lực.
Lời giải chi tiết:
M = F.d = 8a.sin60 o ≈ 1,38 N.m.