Ôn tập chương IV trang 52, 53 SBT Vật lí 10 Kết nối tri thức với cuộc sống
Một động cơ điện được thiết kế để kéo một thùng than khối lượng 400 kg từ dưới mỏ có độ sâu 1200 m lên mặt đất trong thời gian 2 phút. Hiệu suất của động cơ là 80%. Lấy g = 9,8 m/s2. Công suất toàn phần của động cơ là
IV.1
Một động cơ điện được thiết kế để kéo một thùng than khối lượng 400 kg từ dưới mỏ có độ sâu 1200 m lên mặt đất trong thời gian 2 phút. Hiệu suất của động cơ là 80%. Lấy g = 9,8 m/s 2 . Công suất toàn phần của động cơ là
A. 7,8 kW. B. 9,8 kW. C. 31 kW. D. 49 kW.
Phương pháp giải:
Vận dụng công thức tính hiệu suất: H = \(\frac{{{P_i}}}{{{P_{tp}}}}.100\% \).
Lời giải chi tiết:
Đổi t = 2 phút = 120 s.
Công suất dùng để kéo thùng than lên là:
𝒫 ích = \(\frac{{{A_{ich}}}}{t}\)= \(\frac{{P.s}}{t}\)= \(\frac{{400.9,8.1200}}{{120}}\)= 39200 J.
Áp dụng công thức tính hiệu suất ta có: H = \(\frac{{{P_i}}}{{{P_{tp}}}}.100\% \) = 80%.
à 𝒫 tp = \(\frac{{{P_{ich}}}}{{0,8}}\)= \(\frac{{39200}}{{0,8}}\) = 49k J.
Vậy công suất toàn phần của động cơ là 49k J.
Chọn đáp án D.
IV.2
Khi quạt điện hoạt động thì phần năng lượng hao phí là
A. điện năng. B. cơ năng. C. nhiệt năng. D. hoá năng.
Phương pháp giải:
Nắm được đặc điểm của các dạng năng lượng và sự chuyển hóa qua lại giữa chúng.
Lời giải chi tiết:
Khi quạt điện hoạt động thì điện năng được chuyển hóa thành phần năng lượng có ích là động năng và một phần năng lượng hao phí là nhiệt năng làm cho quạt nóng lên.
Chọn đáp án C.
IV.3
Khi con lắc đồng hồ dao động thì
A. Cơ năng của nó bằng không.
B. động năng và thế năng được chuyển hoá qua lại lẫn nhau nhờ công của lực căng dây treo.
C. động năng và thế năng được chuyển hoá qua lại lẫn nhau nhờ công của trọng lực.
D. động năng và thế năng được chuyển hoá qua lại lẫn nhau nhờ công của lực ma sát.
Phương pháp giải:
Áp dụng định luật bảo toàn cơ năng.
Lời giải chi tiết:
Theo định luật bảo toàn cơ năng: Khi một vật chuyển động trong trọng trường chỉ chịu tác dụng của trọng lực thì cơ năng của vật được bảo toàn. Do đó:
Khi con lắc đồng hồ dao động thì động năng và thế năng được chuyển hoá qua lại lẫn nhau là nhờ công của trọng lực.
Chọn đáp án C.
IV.4
Một thùng hàng được đặt trên mặt phẳng nhẵn, nằm ngang. Để dịch chuyển nó, người ta móc dây nối với nó và kéo dây theo phương hợp với phương nằm ngang một góc θ và kéo bởi lực có độ lớn 45 N. Sau khi đi được quãng đường 1,5 m thì lực thực hiện công 50 J và thùng hàng đạt vận tốc 2,6 m/s.
a) Tính góc θ.
b) Tính khối lượng của thùng hàng.
Phương pháp giải:
a) Áp dụng công thức tính công của lực: A = F.s.cosα à cosα = \(\frac{A}{{F.s}}\).
b) Vì mặt sàn nhẵn, nằm ngang nên công của lực kéo chuyển hóa thành động năng của thùng hàng: A k = W đ = 0,5mv 2 à m = \(\frac{{2{A_k}}}{{{v^2}}}\).
Lời giải chi tiết:
a) Công của lực kéo là: A k = F k .s.cosθ à cosθ = \(\frac{{{A_k}}}{{{F_k}.s}}\)= \(\frac{{50}}{{45.1,5}}\) è θ ≈ 42 o .
b) Vì mặt sàn nhẵn, nằm ngang nên công của lực kéo chuyển hóa thành động năng của thùng hàng: A k = W đ = 0,5mv 2 à m = \(\frac{{2{A_k}}}{{{v^2}}}\) = \(\frac{{2.50}}{{2,{6^2}}}\) ≈ 14,8 kg.
IV.5
Một con nhện có khối lượng 0,42 g bò trên bề mặt kính cửa sổ một ngôi nhà với tốc độ không đối 2,3 cm/s theo hướng hợp với phương thẳng đứng một góc như Hình V.1. Lấy gia tốc trọng trường g = 9,8 m/s 2 . Tính công suất của con nhện.

Phương pháp giải:
Áp dụng công thức liên hệ giữa lực và vận tốc: 𝒫 = F.v.
Lời giải chi tiết:
Đổi m = 0,42 g = 0,42.10 -3 kg.
Độ lớn của lực F là: F = \(\frac{P}{{\cos \alpha }}\).
Áp dụng công thức liên hệ giữa lực và vận tốc:
𝒫 = F.v = \(\frac{P}{{\cos \alpha }}\).v = \(\frac{{0,{{42.10}^{ - 3}}.9,8}}{{\cos {{25}^o}}}.2,3\) ≈ 0,01 W.
Vậy công suất của con nhện là 0,01 W.
IV.6
Khi tàu vũ trụ Apollo đổ bộ xuống Mặt Trăng vào ngày 20/7/1969, phi hành gia Neil Armstrong đã được trải nghiệm hiệu ứng hấp dẫn yếu. Ông thực hiện củ nhảy từ bề mặt Mặt Trăng với vận tốc 1,51 m/s và đạt được độ cao 0,7 m. Hãy tính gia tốc trọng trường ở bề mặt Mặt Trăng.
Phương pháp giải:
Áp dụng định luật bảo toàn cơ năng ở vị trí nhảy và ở độ cao 0,7 m.
Lời giải chi tiết:
Chọn mốc thế năng ở bề mặt Mặt trăng.
Cơ năng của phi hành gia ở vị trí nhảy: W 1 = \(\frac{1}{2}m{v^2}\).
Cơ năng của phi hành gia ở độ cao 0,7 m: W 2 = mg MT .h.
Áp dụng định luật bảo toàn cơ năng, ta có: W 1 = W 2
ó \(\frac{1}{2}m{v^2}\) = mg MT .h => g MT = \(\frac{{{v^2}}}{{2h}}\)= \(\frac{{1,{{51}^2}}}{{2.0,7}}\)≈ 1,63 m/s 2 .
Vậy gia tốc trọng trường ở bề mặt Mặt Trăng là 1,63 m/s 2 .
IV.7
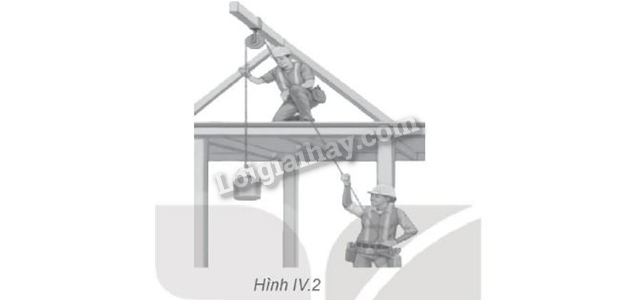
Trên công trường xây dựng, người công nhân sử dụng ròng rọc để đưa vật liệu lên cao (Hình IV.2). Do ảnh hưởng của thời tiết nên hệ thống ròng rọc và dây nối bị bẩn và gỉ sét. Người công nhân phải dùng lực có độ lớn 90 N để nâng vật có trọng lượng 70 N lên độ cao 8 m. Tính hiệu suất của ròng rọc.
Phương pháp giải:
Áp dụng công thức tính hiệu suất: H = \(\frac{{{A_i}}}{{{A_{tp}}}}.100\% \).
Lời giải chi tiết:
Hiệu suất của ròng rọc là: H = \(\frac{{{A_i}}}{{{A_{tp}}}}.100\% \) = \(\frac{{P.s}}{{F.s}}.100\% \) = \(\frac{{70.8}}{{90.8}}.100\% \) ≈ 77,78 %.
IV.8
Một cái bánh mì bơ cung cấp năng lượng 415 cal. Một người có khối lượng 60 kg ăn hết một chiếc bánh mì này rồi leo núi. Tính độ cao tối đa mà người này leo lên được. Biết hiệu suất chuyển hoá năng lượng thành cơ năng của người trung bình là 17% và gia tốc trọng trường là g = 9,8 m/s 2 .
Phương pháp giải:
Tính phần năng lượng chuyển hóa thành cơ năng.
Người này leo được độ cao tối đa khi toàn bộ cơ năng chuyển hóa thành thế năng: W = W t = mgh à h = \(\frac{{\rm{W}}}{{mg}}\).
Lời giải chi tiết:
Năng lượng chuyển hóa thành cơ năng để leo núi là:
W = 415.4,2.17% = 846,6 J.
Độ cao tối đa mà người đó leo lên được là: h = \(\frac{{\rm{W}}}{{mg}}\)= \(\frac{{846,6}}{{60.9,8}}\)≈ 1,44 m.