Giải Thử thách trang 73 SGK Toán 10 tập 2 – Chân trời sáng tạo
Áp dụng tính chất quang học của parabol để giải quyết vẫn đề sau đây:
Đề bài
Áp dụng tính chất quang học của parabol để giải quyết vẫn đề sau đây:
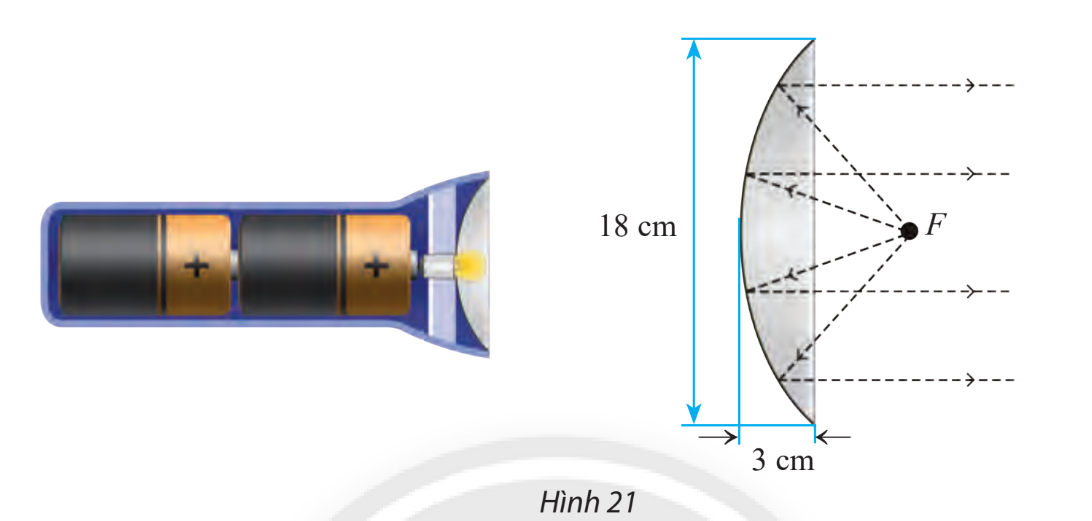
Một đèn pin có chóa đèn có mặt cắt hình parabol với kích thước như trong hình 21.
a) Chọn hệ trục tọa độ Oxy sao cho gốc O là đỉnh của parabol và trục Ox đi qua tiêu điểm. Viết phương trình của parabol trong hệ tọa độ vừa chọn.
b) Để đèn chiếu được xa phải đặt bóng đèn cách đỉnh của chóa đèn bao nhiêu xentimét
Phương pháp giải - Xem chi tiết
a) Bước 1: Gọi phương trình parabol tổng quát \({y^2} = 2px\)
Bước 2: Từ giả thiết \(x = 3,2y = 18\) thay vào phương trình tìm phương trình
b) Xác định tọa độ tiêu điểm
Lời giải chi tiết
a) Vẽ lại hình vẽ như dưới đây
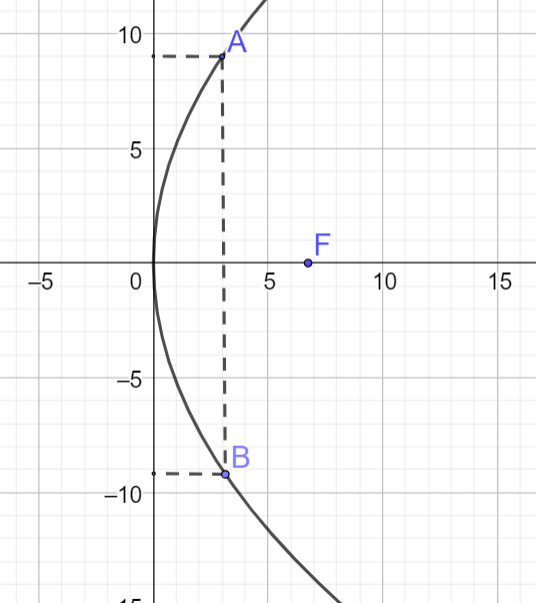
Ta có \(AB = 18,x = 3 \Rightarrow A(3;9)\)
Gọi phương trình parabol tổng quát \({y^2} = 2px\)
Thay tọa độ điểm A vào phương trình ta có: \({9^2} = 2p.3 \Rightarrow p = \frac{{27}}{2}\)
Vậy phương trình parabol trên hệ trục tọa độ vừa chọn là \({y^2} = 27x\)
b) Từ câu a) ta có: \(p = \frac{{27}}{2}\)
Suy ra tiêu điểm của parabol là \(F\left( {\frac{{27}}{4};0} \right)\)
Vậy để đèn chiếu được xa phải đặt bóng đèn cách đỉnh của chóa đèn \(\frac{{27}}{4}\) xentimét