Giải Toán lớp 5 Bài 13. Phép cộng phân số - Bình Minh — Không quảng cáo

Câu 1

Trả lời câu hỏi 1 trang 18 SGK Toán 5 Bình minh

Tính:

Phương pháp giải:

Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số rồi cộng hai phân số đã quy đồng.

Lời giải chi tiết:

a) $\frac{1}{2} + \frac{2}{3} = \frac{3}{6} + \frac{4}{6} = \frac{7}{6}$

b) $\frac{3}{4} + \frac{2}{3} = \frac{9}{{12}} + \frac{8}{{12}} = \frac{{17}}{{12}}$

c) $\frac{3}{5} + \frac{3}{7} = \frac{{21}}{{35}} + \frac{{15}}{{35}} = \frac{{36}}{{35}}$

Câu 2

Trả lời câu hỏi 2 trang 18 SGK Toán 5 Bình minh

<, >, = ?

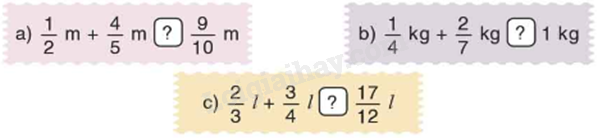
Phương pháp giải:

Tính giá trị của biểu thức rồi so sánh hai vế với nhau.

Lời giải chi tiết:

a) Ta có: $\frac{1}{2} + \frac{4}{5} = \frac{5}{{10}} + \frac{8}{{10}} = \frac{{13}}{{10}}$. Mà $\frac{{13}}{{10}}m > \frac{9}{{10}}m$

Vậy $\frac{1}{2}m + \frac{4}{5}m > \frac{9}{{10}}m$

b) Ta có: $\frac{1}{4} + \frac{2}{7} = \frac{7}{{28}} + \frac{8}{{28}} = \frac{{15}}{{28}}$. Mà $\frac{{15}}{{28}}kg < 1kg$

Vậy $\frac{1}{4}kg + \frac{2}{7}kg < 1kg$

c) Ta có: $\frac{2}{3} + \frac{3}{4} = \frac{8}{{12}} + \frac{9}{{12}} = \frac{{17}}{{12}}$. Mà $\frac{{17}}{{12}}l = \frac{{17}}{{12}}l$

Vậy $\frac{2}{3}l + \frac{3}{4}l = \frac{{17}}{{12}}l$

Câu 3

Trả lời câu hỏi 3 trang 18 SGK Toán 5 Bình minh

Một ô tô chạy từ A đến B, giờ đầu chạy được $\frac{3}{7}$quãng đường, giờ thứ hai chạy được $\frac{1}{2}$quãng đường. Hỏi sau hai giờ, ô tô chạy được bao nhiêu phần của quãng đường?

Phương pháp giải:

Số phần quãng đường ô tô chạy được sau hai giờ = số phần quãng đường ô tô chạy được trong giờ đầu + số phần quãng đường ô tô chạy được trong giờ thứ hai.

Lời giải chi tiết:

Tóm tắt:

Giờ đầu chạy được: $\frac{3}{7}$quãng đường

Giờ thứ hai chạy được: $\frac{1}{2}$quãng đường

Sau hai giờ, ô tô chạy được: ? phần của quãng đường

Số phần quãng đường ô tô chạy được sau hai giờ là:

$\frac{3}{7} + \frac{1}{2} = \frac{{13}}{{14}}$ (quãng đường)

Đáp số: $\frac{{13}}{{14}}$ quãng đường.