Toán lớp 5 Bài 6. Cộng, trừ hai phân số khác mẫu số - SGK kết nối tri thức
Có hai vòi nước cùng chảy vào một bể. Vòi thứ nhất chảy được 1/2 bể, Chọn dấu “+”, dấu “ –” thích hợp thay cho dấu “?”Để chia đều 5 chiếc bánh cho 6 người, hai bạn Nam và Rô-bốt đã đề xuất cách làm như hình
Hoạt động Câu 1
Trả lời câu hỏi 1 phần Hoạt động trang 21 SGK Toán 5 Kết nối tri thức
Tính.
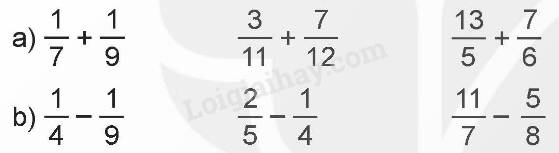
Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Lời giải chi tiết:
a) $\frac{1}{7} + \frac{1}{9} = \frac{9}{{63}} + \frac{7}{{63}} = \frac{{16}}{{63}}$
$\frac{3}{{11}} + \frac{7}{{12}} = \frac{{36}}{{132}} + \frac{{77}}{{132}} = \frac{{113}}{{132}}$
$\;\frac{{13}}{5} + \frac{7}{6} = \frac{{78}}{{30}} + \frac{{35}}{{30}} = \frac{{113}}{{30}}$
b) $\frac{1}{4} - \frac{1}{9} = \frac{9}{{36}} - \frac{4}{{36}} = \frac{5}{{36}}$
$\frac{2}{5} - \frac{1}{4} = \frac{8}{{20}} - \frac{5}{{20}} = \frac{3}{{20}}$
$\frac{{11}}{7} - \frac{5}{8} = \frac{{88}}{{56}} - \frac{{35}}{{56}} = \frac{{53}}{{56}}$
Hoạt động Câu 2
Trả lời câu hỏi 2 phần Hoạt động trang 21 SGK Toán 5 Kết nối tri thức
Có hai vòi nước cùng chảy vào một bể. Vòi thứ nhất chảy được $\frac{1}{2}$ bể, vòi thứ hai chảy được $\frac{2}{5}$ bể. Hỏi cả hai vòi chảy được bao nhiêu phần bể nước?
Phương pháp giải:
Hai vòi chảy được số phần bể nước = số phần bể vòi thứ nhất chảy được + số phần bể vòi thứ hai chảy được.
Lời giải chi tiết:
Tóm tắt
Vòi thứ nhất: $\frac{1}{2}$ bể
Vòi thứ hai: $\frac{2}{5}$ bể
Cả hai vòi: ? bể
Bài giải
Hai vòi chảy được số phần bể nước là:
$\frac{1}{2} + \frac{2}{5} = \frac{9}{{10}}$ (bể)
Đáp số: $\frac{9}{{10}}$ bể nước
Luyện tập Câu 1
Trả lời câu hỏi 1 phần Luyện tập trang 21 SGK Toán 5 Kết nối tri thức
Tính.

Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Lời giải chi tiết:
a) $\frac{6}{{11}} + \frac{1}{2} = \frac{{12}}{{22}} + \frac{{11}}{{22}} = \frac{{23}}{{22}}$
b) $\frac{3}{{10}} + \frac{5}{{21}} = \frac{{63}}{{210}} + \frac{{50}}{{210}} = \frac{{113}}{{210}}$
c) $\frac{{11}}{4} - \frac{7}{5} = \frac{{55}}{{20}} - \frac{{28}}{{20}} = \frac{{27}}{{20}}$
d) $\frac{{20}}{{18}} - \frac{2}{5} = \frac{{10}}{9} - \frac{2}{5} = \frac{{50}}{{45}} - \frac{{18}}{{45}} = \frac{{32}}{{45}}$
Luyện tập Câu 2
Trả lời câu hỏi 2 phần Luyện tập trang 21 SGK Toán 5 Kết nối tri thức
Chọn dấu “+”, dấu “ –” thích hợp thay cho dấu “?”.

Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Lời giải chi tiết:
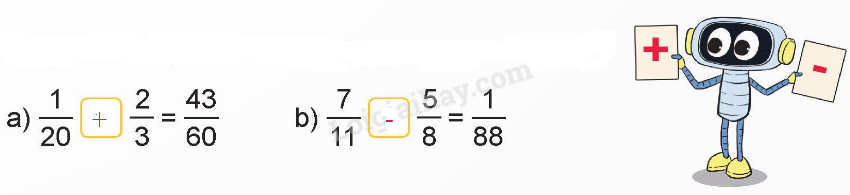
Luyện tập Câu 3
Trả lời câu hỏi 3 phần Luyện tập trang 22 SGK Toán 5 Kết nối tri thức
Tính.

Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Lời giải chi tiết:
a) $7 + \frac{1}{5} = \frac{{35}}{5} + \frac{1}{5} = \frac{{36}}{5}$ b) $\frac{{14}}{5} + 1 = \frac{{14}}{5} + \frac{5}{5} = \frac{{19}}{5}$
c) $3 - \frac{{11}}{8} = \frac{{24}}{8} - \frac{{11}}{8} = \frac{{13}}{8}$
d) $\frac{{31}}{{10}} - 2 = \frac{{31}}{{10}} - \frac{{20}}{{10}} = \frac{{11}}{{10}}$
Luyện tập Câu 4
Trả lời câu hỏi 4 phần Luyện tập trang 22 SGK Toán 5 Kết nối tri thức
Để chia đều 5 chiếc bánh cho 6 người, hai bạn Nam và Rô-bốt đã đề xuất cách làm như hình dưới đây (phần bánh của mỗi người thể hiện bằng các phần tô màu đỏ).
a) Em hãy mô tả cách chia bánh của mỗi bạn.
b) Em hãy giải thích vì sao với cách chia bánh của Rô-bốt thì mỗi bạn được $\frac{5}{6}$ cái bánh.

Phương pháp giải:
Quan sát hình vẽ để mô tả cách chia bánh của mỗi bạn
Lời giải chi tiết:
a) Bạn Nam chia mỗi chiếc bánh thành 6 phần bằng nhau. Mỗi người được nhận 1 phần trên mỗi chiếc bánh đó.
Bạn Rô-bốt chia chiếc bánh thứ nhất thành 2 phần, chiếc bánh thứ hai thành 3 phần. Mỗi người được nhận 1 phần trên mỗi chiếc bánh đó.
b) Ta có $\frac{1}{2} + \frac{1}{3} = \frac{5}{6}$
Vậy với cách chia bánh của Rô-bốt thì mỗi bạn được $\frac{5}{6}$ cái bánh.