Bài 3. Thực hành tính sai số trong phép đo. Ghi kết quả đo trang 17, 18, 19 Vật Lí 10 Kết nối tri thức
Em hãy lập phương án đo tốc độ chuyển động của chiếc xe ô tô đồ chơi chỉ dùng thước; đồng hồ bấm giây và trả lời các câu hỏi sau. Để đo tốc độ chuyển động của chiếc xe cần đo đại lượng nào. Xác định tốc độ chuyển động của xe theo công thức nào. Phép đo nào là phép đo trực tiếp. Tại sao. Phép đo nào là phép đo gián tiếp. Tại sao. Dùng một thước có ĐCNN là 1 mm và một đồng hồ đo thời gian có ĐCNN 0,01s để đo 5 lần thời gian chuyển động của chiếc xe đồ chơi chạy bằng pin từ điểm A (vA = 0) đến điểm
Câu hỏi tr 17
|
Em hãy lập phương án đo tốc độ chuyển động của chiếc xe ô tô đồ chơi chỉ dùng thước; đồng hồ bấm giây và trả lời các câu hỏi sau: a) Để đo tốc độ chuyển động của chiếc xe cần đo đại lượng nào? b) Xác định tốc độ chuyển động của xe theo công thức nào? c) Phép đo nào là phép đo trực tiếp? Tại sao? d) Phép đo nào là phép đo gián tiếp? Tại sao? |
Phương pháp giải:
Vận dụng các kiến thức đã học về vận tốc.
Lời giải chi tiết:
* Phương án:
- Dụng cụ: ô tô đồ chơi, thước, đồng hồ bấm giây.
- Cách tiến hành:
+ Chọn vạch xuất phát làm mốc, cho ô tô bắt đầu chuyển động
+ Dùng đồng hồ bấm giây để xác định thời gian từ lúc ô tô bắt đầu chuyển động đến khi ô tô dừng lại
+ Dùng thước đo quãng đường từ vạch xuất phát đến điểm ô tô dừng lại.
a) Để đo tốc độ chuyển động của chiếc xe cần đo các đại lượng là: Thời gian (t) và quãng đường (s).
b) Xác định tốc độ chuyển động của chiếc xe bằng công thức: \(v = \frac{s}{t}\)
c) Phép đo thời gian và quãng đường là phép đo trực tiếp vì chúng lần lượt được đo bằng dụng cụ đo là đồng hồ và thước. Kết quả của phép đo được đọc trực tiếp trên dụng cụ đo.
d) Phép đo tốc độ là phép đo gián tiếp vì nó được xác định thông qua công thức liên hệ với các đại lượng được đo trực tiếp là quãng đường và thời gian.
Câu hỏi tr19
|
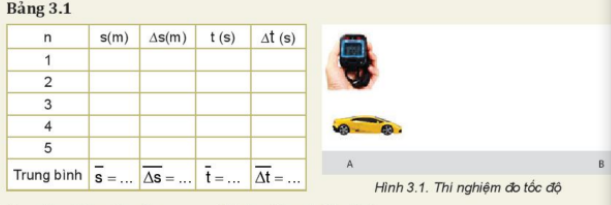
Dùng một thước có ĐCNN là 1 mm và một đồng hồ đo thời gian có ĐCNN 0,01s để đo 5 lần thời gian chuyển động của chiếc xe đồ chơi chạy bằng pin từ điểm A (v A = 0) đến điểm B (Hình 3.1). Ghi các giá trị vào Bảng 3.1 và trả lời các câu hỏi.
a) Nguyên nhân nào gây ra sự sai khác giữa các lần đo? b) Tính sai số tuyệt đối của phép đo s, t và điền vào Bảng 3.1. c) Viết kết quả đo: s = …..; t = ….. d) Tính sai số tỉ đối: \(\delta t = \frac{{\Delta t}}{{\overline t }}.100\% = ...;\delta s = \frac{{\Delta s}}{{\overline s }}.100\% = ...\) \(\delta v = ...;\,\Delta v = ...\) |
Phương pháp giải:
- Tiến hành thí nghiệm theo yêu cầu của đề bài.
- Sử dụng các công thức tính sai số để trả lời câu hỏi.
Lời giải chi tiết:
Bảng kết quả tham khảo:
|
n |
s (m) |
Δs (m) |
t (s) |
Δt (s) |
|
1 |
0,649 |
0,0024 |
3,49 |
0.024 |
|
2 |
0,651 |
0,0004 |
3,51 |
0,004 |
|
3 |
0,654 |
0,0026 |
3,54 |
0,026 |
|
4 |
0,653 |
0,0016 |
3,53 |
0,016 |
|
5 |
0,650 |
0,0014 |
3,50 |
0,014 |
|
Trung bình |
\(\overline s = 0,6514\) |
\(\overline {\Delta s} = 0,00168\) |
\(\overline t = 3,514\) |
\(\overline {\Delta t} = 0,0168\) |
a) Nguyên nhân gây ra sự sai khác giữa các lần đo là:
- Do đặc điểm và cấu tạo của dụng cụ đo
- Do điều kiện làm thí nghiệm chưa được chuẩn
- Do thao tác khi đo
b) Ta có:
\(\overline {\Delta s} = \frac{{\left| {\overline s - {s_1}} \right| + \left| {\overline s - {s_2}} \right| + ... + \left| {\overline s - {s_5}} \right|}}{5} = 0,00168\)
\(\overline {\Delta t} = \frac{{\left| {\overline t - {t_1}} \right| + \left| {\overline t - {t_2}} \right| + ... + \left| {\overline t - {t_5}} \right|}}{5} = 0,0168\)
c) Viết kết quả đo:
Ta có:
\(\Delta s = \overline {\Delta s} + \Delta {s_{dc}} = 0,00168 + \frac{{0,001}}{2} = 0,00218\)
\(\Delta t = \overline {\Delta t} + \Delta {t_{dc}} = 0,0168 + \frac{{0,01}}{2} = 0,0218\)
Suy ra:
\(s = \overline s \pm \Delta s = 0,6514 \pm 0,00218\left( m \right)\)
\(t = \overline t \pm \Delta t = 3,514 \pm 0,0218\left( s \right)\)
d) Tính sai số tỉ đối:
\(\delta t = \frac{{\Delta t}}{{\overline t }}.100\% = \frac{{0,0218}}{{3,514}}.100\% = 0,620\)
\(\delta s = \frac{{\Delta s}}{{\overline s }}.100\% = \frac{{0,00218}}{{0,6514}}.100\% = 0,335\)
\(\delta v = \frac{{\Delta s}}{{\overline s }}.100\% + \frac{{\Delta t}}{{\overline t }}.100\% = 0,335 + 0,620 = 0,955\)
\(\Delta v = \delta v.\overline v = 0,955.\frac{{0,6514}}{{3,514}} = 0,177\left( {m/s} \right)\)