Lý thuyết Các phép toán với số hữu tỉ SGK Toán 7 - Chân trời sáng tạo
1. Cộng và trừ hai số hữu tỉ
1. Cộng và trừ hai số hữu tỉ
a) Cộng, trừ hai số hữu tỉ
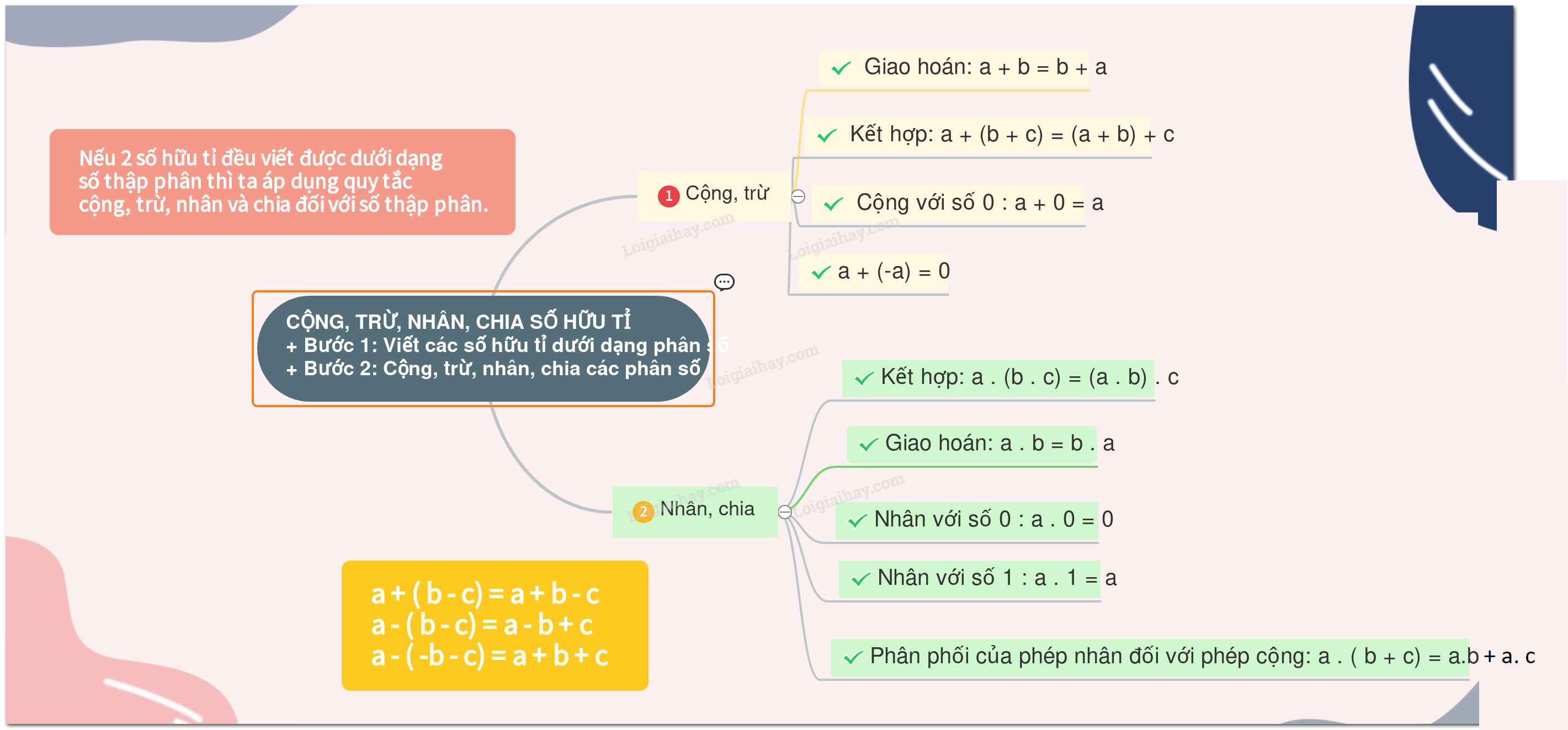
+ Bước 1: Viết các số hữu tỉ dưới dạng phân số
+ Bước 2: Cộng, trừ phân số
Chú ý: Nếu 2 số hữu tỉ đều viết được dưới dạng số thập phân thì ta áp dụng quy tắc cộng và trừ 2 đối với số thập phân.
* Tính chất của phép cộng số hữu tỉ:
+ Giao hoán: a + b = b + a
+ Kết hợp: a + (b + c) = (a + b) + c
+ Cộng với số 0 : a + 0 = a
+ 2 số đối nhau luôn có tổng là 0: a + (-a) = 0
Chú ý: * Trong tập các số hữu tỉ Q, ta cũng có quy tắc dấu ngoặc tương tự như trong tập các số nguyên Z:
Khi bỏ ngoặc,
+ Nếu trước dấu ngoặc có dấu “+” thì ta bỏ ngoặc và giữ nguyên dấu của tất cả các số hạng trong ngoặc.
+ Nếu trước dấu ngoặc có dấu “-” thì ta bỏ ngoặc và đổi dấu tất cả các số hạng trong ngoặc.
* Đối với 1 tổng, ta có thể đổi chỗ tùy ý các số hạng, đặt dấu ngoặc để nhóm các số hạng 1 cách tùy ý.
Ví dụ:
\(\begin{array}{l}\frac{8}{5} - (\frac{5}{4} + \frac{3}{5} - \frac{1}{4})\\ = \frac{8}{5} - \frac{5}{4} - \frac{3}{5} + \frac{1}{4}\\ = \left( {\frac{8}{5} - \frac{3}{5}} \right) + \left( {\frac{1}{4} - \frac{5}{4}} \right)\\ = \frac{5}{5} + \frac{{ - 4}}{4}\\ = 1 + ( - 1)\\ = 0\end{array}\)
2. Nhân hai số hữu tỉ
+ Bước 1: Viết hai số hữu tỉ dưới dạng phân số
+ Bước 2: Nhân hai phân số:
\(\frac{a}{b}.\frac{c}{d} = \frac{{a.c}}{{b.d}}(b,d \ne 0)\)
Chú ý: Nếu 2 số hữu tỉ đều viết được dưới dạng số thập phân thì ta áp dụng quy tắc nhân đối với số thập phân.
3. Tính chất của phép nhân số hữu tỉ:
+ Giao hoán: a . b = b . a
+ Kết hợp: a . (b . c) = (a . b) . c
+ Nhân với số 0 : a . 0 = 0
+ Nhân với số 1 : a . 1 = a
+ Tính chất phân phối của phép nhân đối với phép cộng: a . ( b + c) = a.b + a.c
4. Chia 2 số hữu tỉ
+ Bước 1: Viết hai số hữu tỉ dưới dạng phân số
+ Bước 2: Nhân hai phân số: \(\frac{a}{b}:\frac{c}{d} = \frac{a}{b}.\frac{d}{c} = \frac{{a.d}}{{b.c}}(b,c,d \ne 0)\)
Ví dụ:
\(\begin{array}{l}\frac{4}{7}.\frac{3}{5} - \frac{2}{5}:\frac{7}{{ - 4}}\\ = \frac{4}{7}.\frac{3}{5} - \frac{2}{5}.\frac{{ - 4}}{7}\\ = \frac{4}{7}.\frac{3}{5} + \frac{4}{7}.\frac{2}{5}\\ = \frac{4}{7}.\left( {\frac{3}{5} + \frac{2}{5}} \right)\\ = \frac{4}{7}.1\\ = \frac{4}{7}\end{array}\)