Lý thuyết Đoạn thẳng Toán 6 Cánh diều — Không quảng cáo

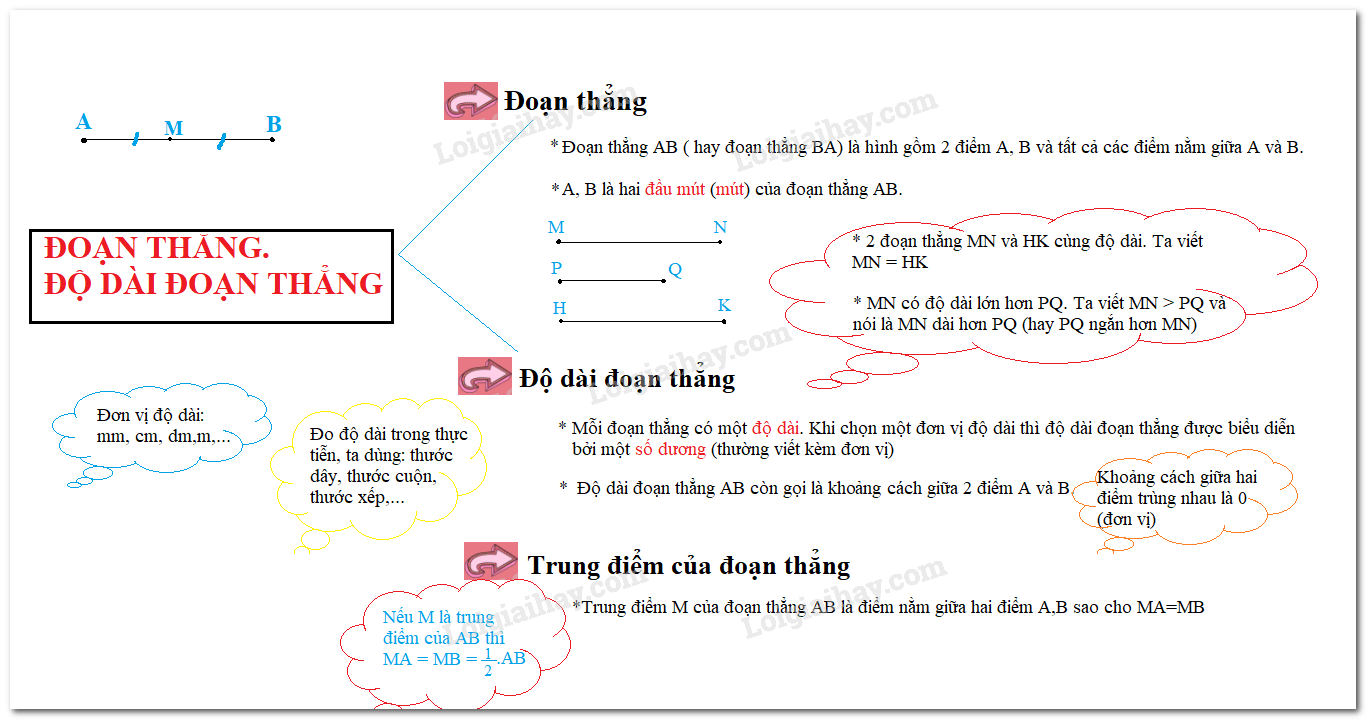
I. Đoạn thẳng

Đoạn thẳng AB còn gọi là đoạn thẳng BA.

Hai điểm A, B gọi là hai đầu mút (hoặc hai đầu) của đoạn thẳng AB.

Chú ý:

Dấu hiệu nhận biết một điểm nằm giữa hai điểm.

“Nếu điểm \(M\) thuộc đoạn thẳng \(AB\) thì điểm \(M\) nằm giữa hai điểm \(A\) và \(B\)”.

II. Độ dài đoạn thẳng

- Mỗi đoạn thẳng có một độ dài. Độ dài đoạn thẳng là một số dương.

- Độ dài đoạn thẳng AB là khoảng cách giữa hai điểm A và B.

- Nếu hai điểm trùng nhau thì khoảng cách giữa chúng bằng O.

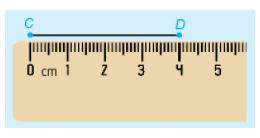
Ví dụ : Đoạn thẳng CD dài 4 cm

III. So sánh hai đoạn thẳng

Ta có thể so sánh hai đoạn thẳng bằng cách so sánh độ dài của chúng.

Ta nói rằng:

- Đoạn thẳng AB bằng đoạn thẳng CD và viết là \(AB = CD\).

- Đoạn thẳng EF dài hơn đoạn thẳng AB và viết là \(EF > AB.\)

- Đoạn thẳng CD ngắn hơn đoạn thẳng EF và viết là \(CD < EF\).

Chú ý:

+ Ta có thể dùng mệnh đề: “Nếu \(AM + MB \ne AB\) thì điểm \(M\) không nằm giữa \(A\) và \(B.\)”

+ Nếu điểm \(M\) nằm giữa \(A\) và \(B;\) điểm \(N\) nằm giữa \(M\) và \(B\) thì \(AM + MN + NB = AB.\)

IV. Trung điểm của đoạn thẳng

Tóm tắt:

\(I\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow $${\rm{IA  =  IB}}$ và \(I\) nằm giữa hai điểm \(A;B.\)

hoặc \(I\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow \left\{ \begin{array}{l}AI + IB = AB\\{\rm{IA  =  IB}}\end{array} \right.$

hoặc \(I\) là trung điểm của đoạn thẳng \(AB\)  $ \Leftrightarrow {\rm{AI  =  BI  = }}\dfrac{1}{2}AB$

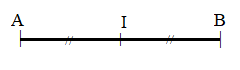
V. Cách vẽ trung điểm của đoạn thẳng

Giả sử ta cần vẽ trung điểm M của đoạn thẳng AB có độ dài 5 cm.

Cách 1:

- Đặt mép thước trung với đoạn thẳng AB sao cho vạch 0 trùng với điểm A, khi đó điểm B trùng với vạch chỉ số 5 trên thước.

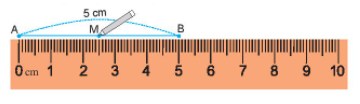
- Ta lấy điểm M trùng với vạch chỉ số 2,5 cm trên thước, Khi đó ta có M là trung điểm của đoạn thẳng AB.

Cách 2:

Vẽ đoạn thẳng AB trên giấy can. Gấp giấy sao cho điểm B trùng với điểm A. Giao của nếp gấp và đoạn thẳng AB chính là trung điểm M cần xác định