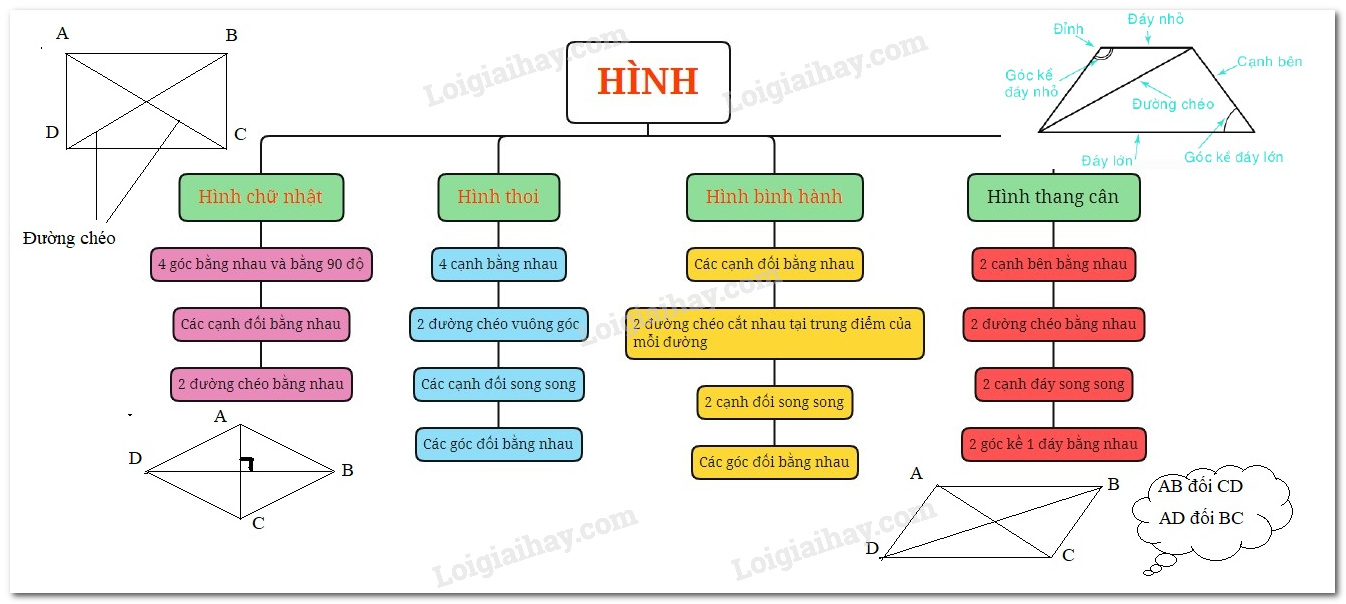
Lý thuyết Hình chữ nhật. Hình thoi. Hình bình hành. Hình thang cân Toán 6 KNTT với cuộc sống
Lý thuyết Hình chữ nhật. Hình thoi. Hình bình hành. Hình thang cân Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
I. Hình chữ nhật
1. Nhận biết hình chữ nhật
Một số yếu tố cơ bản của hình chữ nhật
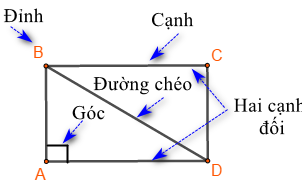
- Bốn góc bằng nhau và bằng \({90^0}\)
- Các cạnh đối bằng nhau.
- Hai đường chéo bằng nhau.
2.Cách vẽ hình chữ nhật
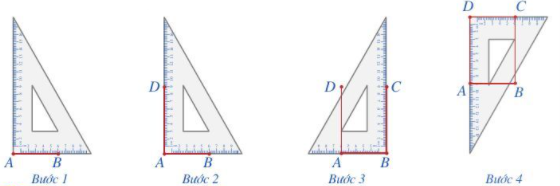
Bước 1 . Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng 6 cm
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng 9 cm
Bước 3 . Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng 9 cm
Bước 4 . Vẽ đoạn thẳng CD.
II. Hình thoi
1. Một số yếu tố cơ bản của hình thoi
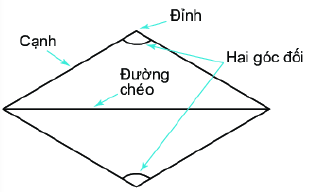
- Bốn cạnh bằng nhau
- Hai đường chéo vuông góc với nhau.
- Các cạnh đối song song với nhau
- Các góc đối bằng nhau
2. Vẽ hình thoi
Ví dụ: Dùng thước và compa vẽ hình thoi \(ABCD\), biết \(AB = 5\,cm\) và \(AC = 8\,cm\).
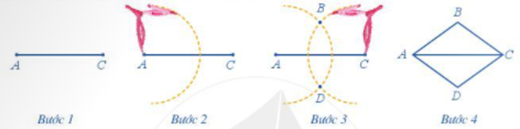
Bước 1 . Dùng thước vẽ đoạn thẳng \(AC = 8\,cm\)
Bước 2 . Dùng compa vẽ một phần đường tròn tâm A bán kính \(5\,cm\).
Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính \(5\,cm\); phần đường tròn này cắt phần đường tròn tấm A vẽ ở Bước 2 tại các điểm B và D.
Bước 4 . Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA.
III. Hình bình hành
1.Nhận biết hình bình hành
Hình bình hành ABCD có:
- Bốn đỉnh A, B, C, D.
- Hai cặp cạnh đối diện bằng nhau: \(AB = CD;\,BC = AD\).
- Hai cặp cạnh đối diện song song: \(AB\) song song với \(CD\); \(BC\) song song với \(AD\).
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: \(OA = OC;\,OB = OD.\)
- Hai góc ở các đỉnh A và C bằng nhau; hai góc ở các đỉnh B và D bằng nhau.
2.Cách vẽ hình bình hành
Ví dụ: Cho trước hai đoạn thẳng AB,AD như hình dưới đây. Vẽ hình bình hành ABCD nhận hai đoạn thẳng AB, AD làm cạnh.

Cách vẽ:
Ta có thể vẽ bằng thước và compa như sau:
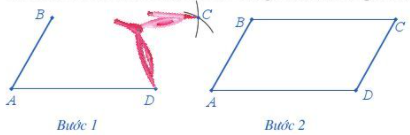
Bước 1 . Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính AD. Lấy D làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB. Gọi C là giao điểm của hai phần đường tròn này
Bước 2 . Dùng thước vẽ các đoạn thẳng BC và CD.
IV. Hình thang cân
1. Nhận biết hình thang cân
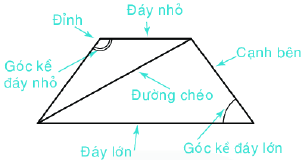
Hình thang cân có:
- Hai cạnh bên bằng nhau.
- Hai đường chéo bằng nhau
- Hai đáy song song với nhau
- Hai góc kề một đáy bằng nhau.
Ví dụ:
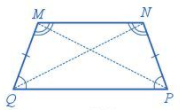
Hình thang cân \(MNPQ\) có:
- Hai cạnh cạnh đáy song song: \(MN\) song song với \(PQ\).
- Hai cạnh bên bằng nhau: \(MQ = NP\).
- Hai đường chéo bằng nhau: \(MP = NQ\).
- Hai góc kề với cạnh cạnh bên \(PQ\) bằng nhau, tức là hai góc \(NPQ\) và \(PQM\) bằng nhau; hai góc kề với cạnh bên \(MN\) bằng nhau, tức là hai góc \(QMN\) và \(MNP\) bằng nhau.
2.Cách gấp hình thang cân
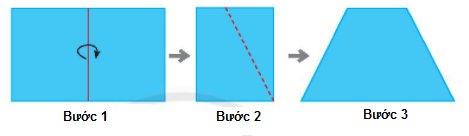
Bước 1 : Gấp đôi một tờ giấy hình chữ nhật
Bước 2 : Vẽ một đoạn thẳng nối hai điểm tùy ý trên hai cạnh đối diện (Cạnh không chứa nếp gấp). Cắt theo đường nét đứt như hình minh họa.
Bước 3 : Mở tờ giấy ra ta được một hình thang cân.