Lý thuyết Làm tròn và ước lượng Toán 6 KNTT với cuộc sống — Không quảng cáo

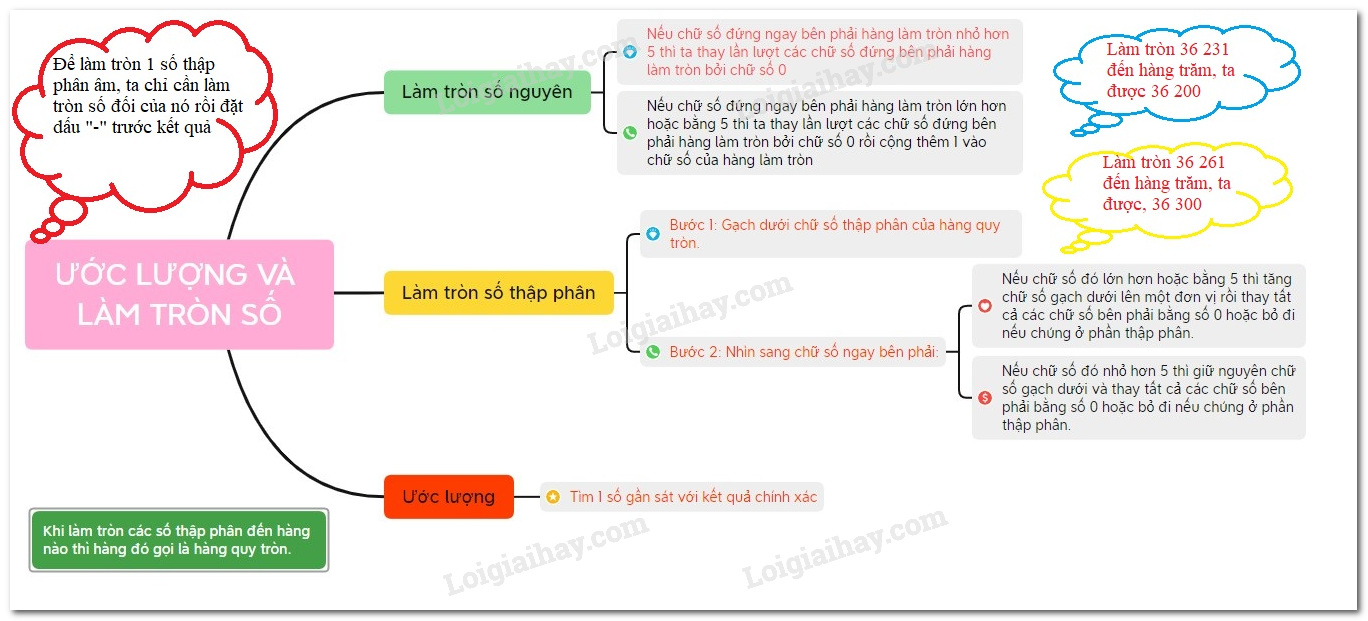
1. Làm tròn

*Làm tròn số thập phân

Để làm tròn số thập phân dương tới một hàng nào đó ( gọi là hàng làm tròn), ta làm như sau:

- Đối với chữ số hàng làm tròn:

+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;

+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5

- Đối với chữ số sau hàng làm tròn:

+ Bỏ đi nếu ở phần thập phân;

+ Thay bằng các chữ số 0 nếu ở phần số nguyên

Ví dụ:

Làm tròn số $24,037$ đến hàng phần mười (đến chữ số thập phân thứ nhất).

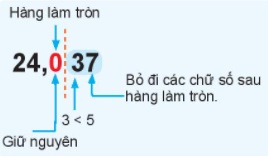
Làm tròn số  đến hàng phần mười ta được kết quả là $24,0$

Vậy: $24,037 \approx 24,0$.

* Làm tròn số nguyên

Nếu chữ số đứng ngay bên phải hàng làm tròn nhỏ hơn 5 thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0

Ví dụ: Số 134 261 làm tròn đến hàng nghìn là số 134 000 ( vì chữ số 2 bên phải hàng nghìn nhỏ hơn 5)

Nếu chữ số đứng ngay bên phải hàng làm tròn lớn hơn hoặc bằng 5 thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0 rồi cộng thêm 1 vào chữ số của hàng làm tròn

Ví dụ: Số 134 761 làm tròn đến hàng nghìn là số 135 000 ( vì chữ số 7 bên phải hàng nghìn lớn hơn 5)

Chú ý: Để làm tròn 1 số thập phân âm, ta chỉ cần làm tròn số đối của nó rồi đặt dấu "-" trước kết quả

Chú ý : Kí hiệu “ \(\approx\)” đọc là “gần bằng” hoặc “xấp xỉ”.

Ví dụ: Làm tròn số $125\,\,356$ đến hàng nghìn

Do chữ số hàng trăm là $3$ nên: $125\,\,356 \approx 125\,\,000$

2. Ước lượng kết quả

Ta có thể sử dụng quy ước làm tròn số để ước lượng kết quả các phép tính. Nhờ đó có thể dễ dàng phát hiện ra những đáp số không hợp lí.

Ví dụ:

Ước lượng kết quả các phép tính sau:

a) $\left( { - 11,032} \right).\left( { - 24,3} \right) \approx 11.24 = 264$

b) $81.49 \approx 80.50 = 4\,000$