Lý thuyết Mở rộng phân số. Phân số bằng nhau Toán 6 KNTT với cuộc sống — Không quảng cáo

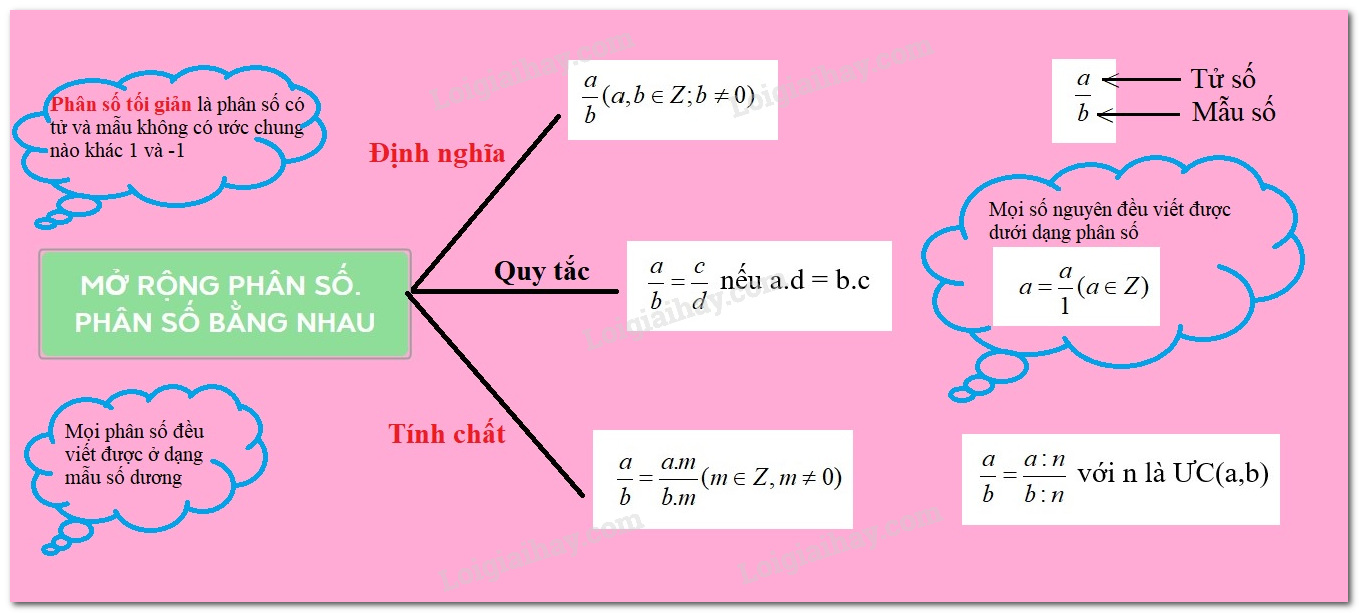
Hai phân số bằng nhau

1. Mở rộng khái niệm phân số

Ta gọi \(\frac{a}{b}\), trong đó \(a,\;b \in \mathbb{Z},\;b \ne 0\)là phân số , a là tử số (tử) và b là mẫu số (mẫu) của phân số. Phân số \(\frac{a}{b}\) đọc là a phần b.

2. Hai phân số bằng nhau

Hai phân số \(\frac{a}{b}\) và \(\frac{c}{d}\) được gọi là bằng nhau , viết là \(\frac{a}{b} = \frac{c}{d}\), nếu \(a.d = b.c\).

Chú ý : Điều kiện \(a.d = b.c\) gọi là điều kiện bằng nhau của hai phân số \(\frac{a}{b}\) và \(\frac{c}{d}\).

3. Tính chất cơ bản của phân số

* Nếu ta nhân cả tử và mẫu của một phân số với cùng 1 số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.

*Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.

Chú ý: Mọi số nguyên a đều viết được dưới dạng phân số:\(\dfrac{a}{1}\)

* Phương pháp rút gọn về phân số tối giản

Bước 1: Tìm ƯCLN của tử và mẫu sau khi đã bỏ dấu – (nếu có)

Bước 2: Chia cả tử và mẫu cho ước chung lớn nhất vừa tìm được, ta có phân số tối giản cần tìm

CÁC DẠNG TOÁN VỀ MỞ RỘNG PHÂN SỐ. PHÂN SỐ BẰNG NHAU

I. Nhận biết phân số, đọc các phân số, mô tả các bài toán thực tiễn qua phân số

- Sử dụng định nghĩa phân số:

Người ta gọi \(\dfrac{a}{b}\) với \(a,b \in Z;b \ne 0\) là một phân số, \(a\) là tử số (tử), \(b\) là mẫu số (mẫu) của phân số.

- Quan sát hình vẽ hoặc dựa vào các dự kiện đề bài ra để mô tả các bài toán thực tiễn qua phân số. Ý nghĩa tử số và mẫu số của phân số: +) Mẫu số cho biết đơn vị được chia ra làm mấy phần bằng nhau +) Tử số cho biết số phần bằng nhau đã lấy.

Chú ý: Mẫu của phân số phải khác 0.

II. Nhận biết các cặp phân số bằng nhau, không bằng nhau

- Nếu \(a.d = b.c\) thì \(\dfrac{a}{b} = \dfrac{c}{d}\) ;

- Nếu \(a.d \ne b.c\) thì \(\dfrac{a}{b} \ne \)\(\dfrac{c}{d}\) ;

III. Tìm số chưa biết trong đẳng thức của hai phân số

Cách 1: \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\) nên \(a.d = b.c\) (định nghĩa hai phân số bằng nhau)

Suy ra \(a = \dfrac{{b.c}}{d}\) , \(d = \dfrac{{b.c}}{a}\) , \(b = \dfrac{{a.d}}{c}\) , \(c = \dfrac{{a.d}}{b}.\)

Cách 2: Áp dụng tính chất cơ bản của phân số để biến đổi hai phân số đã cho thành hai phân số bằng chúng nhưng có từ (hoặc mẫu) như nhau. Khi đó mẫu (hoặc tử) của chúng phải bằng nhau. Từ đó tìm được số chưa biết.

IV. Lập các cặp phân số bằng nhau từ một đẳng thức cho trước

Từ định nghĩa phân số bằng nhau ta có:

\(a.d = b.c\) \( \Rightarrow \) \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\) ;

\(a.d = c.b\) \( \Rightarrow \) \(\dfrac{a}{c}\) = \(\dfrac{b}{d}\) ;

\(d.a = b.c\) \( \Rightarrow \) \(\dfrac{d}{b}\) = \(\dfrac{c}{a}\) ;

\(d.a = c.b\) \( \Rightarrow \) \(\dfrac{d}{c}\) = \(\dfrac{b}{a}\) ;

V. Xác định các phân số bằng nhau

Áp dụng tính chất cơ bản của phân số

$\dfrac{a}{b} = \dfrac{{a.m}}{{b.m}}$ với $m \in Z$ và $m \ne 0$ ; $\dfrac{a}{b} = \dfrac{{a:n}}{{b:n}}$ với $n \in $ ƯC $\left( {a;b} \right)$ .

VI. Viết dạng tổng quát của tất cả các phân số bằng một phân số cho trước

Ta thực hiện hai bước:

- Rút gọn phân số đã cho đến tối giản, chằng hạn ta được phân số tối giản $\dfrac{m}{n}$ ;

- Dạng tổng quát của các phân số phải tìm là $\dfrac{{m.k}}{{n.k}}$ ( $k$ $ \in $ $\mathbb{Z}$ , $k$ $ \ne 0).$