Lý thuyết Lũy thừa với số mũ tự nhiên Toán 6 KNTT với cuộc sống
Lý thuyết Lũy thừa với số mũ tự nhiên Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
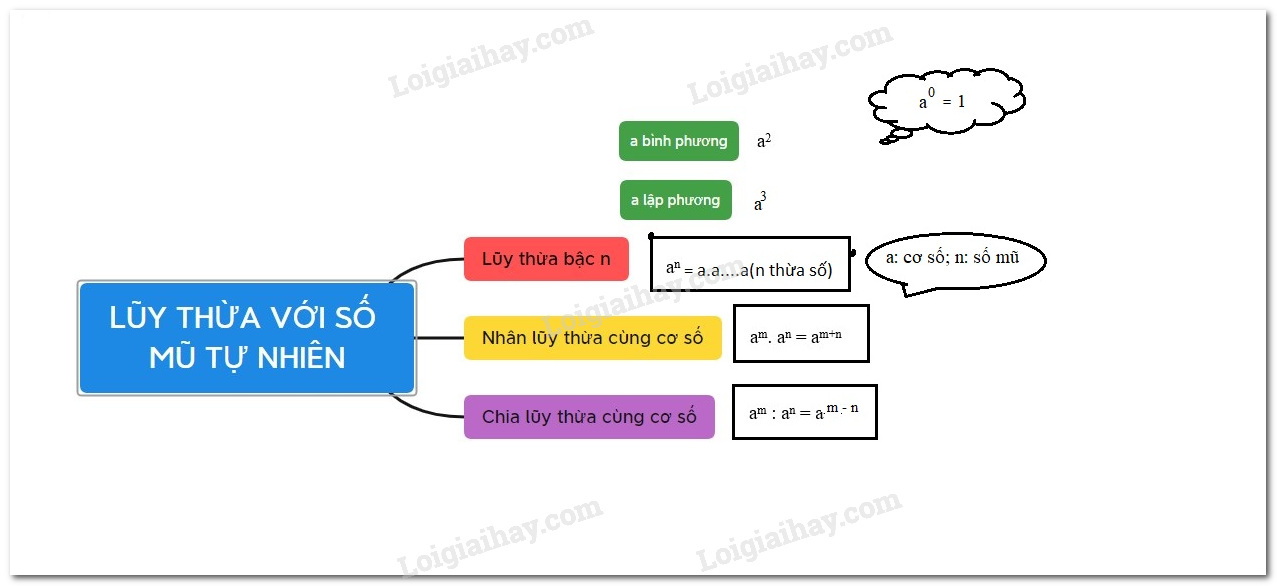
1. Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
\({a^n} = a.a \ldots ..a\) (\(n\) thừa số \(a\) ) (\(n \ne 0\))
\({a^n}\) đọc là “ a mũ n ” hoặc “ a lũy thừa n ”.
\(a\) được gọi là cơ số .
\(n\) được gọi là số mũ .
Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa.
\({a^1} = a\)
\({a^2} = a.a\) gọi là “ \(a\) bình phương” (hay bình phương của \(a\)).
\({a^3} = a.a.a\) gọi là “ \(a\) lập phương” (hay lập phương của \(a\)).
Quy ước: \({a^1} = a\); \({a^0} = 1\left({a \ne 0} \right).\)
Ví dụ: Tính \({2^3}\).
Số trên là lũy thừa bậc 3 của 2 và là tích của 3 thừa số 2 nhân với nhau nên ta có:
\({2^3} = 2.2.2 = 8\)
2. Nhân hai lũy thừa cùng cơ số
\({a^m}.{a^n} = {a^{m + n}}\)
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ .
Ví dụ: \({3.3^5} = {3^1}{.3^5} = {3^{1 + 5}} = {3^6}.\)
3. Chia hai lũy thừa cùng cơ số
\({a^m}:{a^n} = {a^{m - n}}\) \(\left( {a \ne 0;\,m \ge n \ge 0} \right)\)
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau.
Ví dụ: \({3^5}:3 = {3^5}:{3^1} = {3^{5 - 1}} = {3^4} = 3.3.3.3 = 81\)