Lý thuyết Hình trụ Toán 9 Chân trời sáng tạo
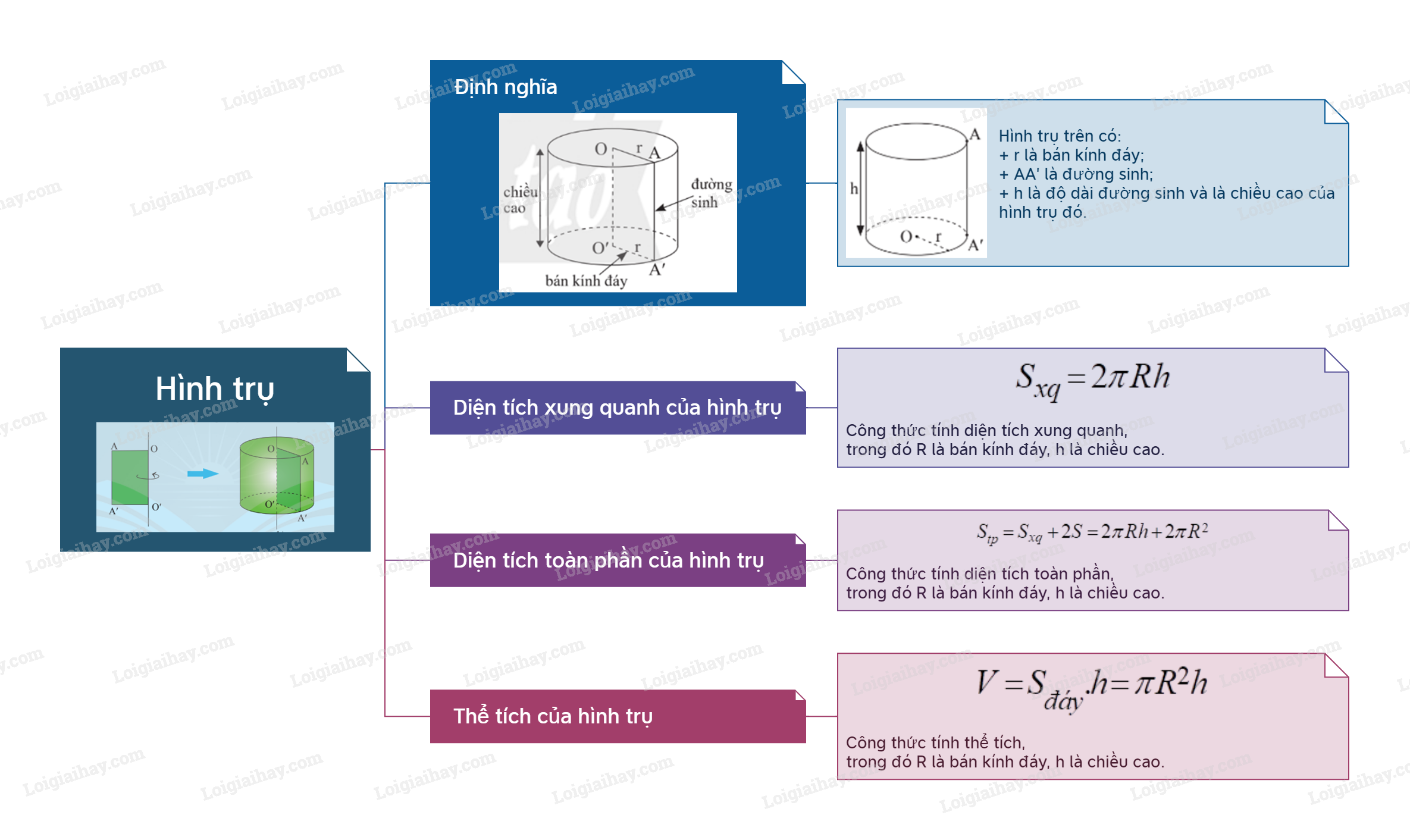
1. Hình trụ Định nghĩa Khi quay hình chữ nhật AA'O'O một vòng quanh cạnh OO' cố định ta được một hình trụ. − Cạnh OA, O′A′ quét thành hai hình tròn có cùng bán kính gọi là hai đáy của hình trụ; bán kính của đáy gọi là bán kính đáy của hình trụ. – Cạnh AA′ quét thành mặt xung quanh của hình trụ, mỗi vị trí của AA' được coi là một đường sinh. – Độ dài đoạn OO' gọi là chiều cao của hình trụ. Các đường sinh có độ dài bằng nhau và bằng chiều cao của hình trụ.
1. Hình trụ
Định nghĩa
|
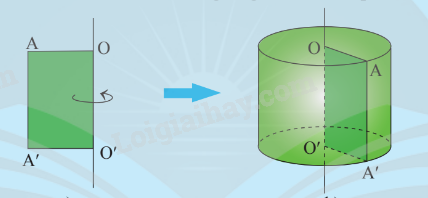
Khi quay hình chữ nhật AA'O'O một vòng quanh cạnh OO' cố định ta được một hình trụ.
− Cạnh OA, O′A′ quét thành hai hình tròn có cùng bán kính gọi là hai đáy của hình trụ; bán kính của đáy gọi là bán kính đáy của hình trụ. – Cạnh AA′ quét thành mặt xung quanh của hình trụ, mỗi vị trí của AA' được coi là một đường sinh. – Độ dài đoạn OO' gọi là chiều cao của hình trụ. Các đường sinh có độ dài bằng nhau và bằng chiều cao của hình trụ. |
Ví dụ:
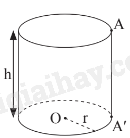
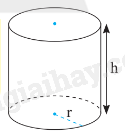
Hình trụ trên có:
+ r là bán kính đáy;
+ AA’ là đường sinh;
+ h là độ dài đường sinh và là chiều cao của hình trụ đó.
2. Diện tích xung quanh của hình trụ
Diện tích xung quanh của hình trụ
|
Diện tích xung quanh \({S_{xq}}\) của hình trụ có bán kính đáy r và chiều cao h là: \({S_{xq}} = 2\pi rh\). |
Diện tích toàn phần của hình trụ
|
Diện tích toàn phần \({S_{tp}}\) của hình trụ có bán kính đáy r và chiều cao h là: \({S_{tp}} = {S_{xq}} + 2S = 2\pi rh + 2\pi {r^2}\) (S là diện tích đáy của hình trụ). |
Ví dụ:
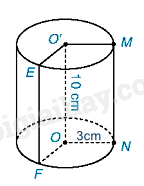
Diện tích xung quanh của hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .3.10 = 60\pi \left( {c{m^2}} \right)\)
3. Thể tích của hình trụ
|
Thể tích V của hình trụ có bán kính đáy r và chiều cao h là: \(V = S.h = \pi {r^2}h\) (S là diện tích đáy của hình trụ).
|
Ví dụ:
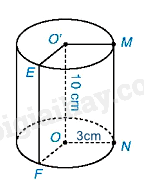
Diện tích đáy là:
\(S = \pi {r^2} = \pi {.3^2} = 9\pi \left( {c{m^2}} \right)\)
Thể tích của hình trụ là:
\(V = S.h = 9\pi .10 = 90\pi \left( {c{m^3}} \right)\)