Lý thuyết Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn Toán 9 Chân trời sáng tạo
1. Phương trình bậc nhất hai ẩn Khái niệm phương trình bậc nhất hai ẩn Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\), trong đó a, b và c là các số đã biết (gọi là hệ số), \(a \ne 0\) hoặc \(b \ne 0\).
1. Phương trình bậc nhất hai ẩn
Khái niệm phương trình bậc nhất hai ẩn
|
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\), trong đó a, b và c là các số đã biết (gọi là hệ số), \(a \ne 0\) hoặc \(b \ne 0\). |
Ví dụ: \(2x + 3y = 4\), \(0x + 2y = 3\), \(x + 0y = 2\) là các phương trình bậc nhất hai ẩn.
Nghiệm của phương trình bậc nhất hai ẩn
|
Nếu giá trị của vế trái tại \(x = {x_0}\) và \(y = {y_0}\) bằng vế phải thì cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của phương trình. Giải hệ phương trình là tìm tất cả các nghiệm của hệ phương trình đó. |
Ví dụ: Cặp số \(( - 1;2)\) là nghiệm của phương trình \(2x + 3y = 4\) vì \(2.\left( { - 1} \right) + 3.2 = - 2 + 6 = 4\).
Cặp số \((1;2)\) không là nghiệm của phương trình \(2x + 3y = 4\) vì
\(2.1 + 3.2 = 2 + 6 = 8 \ne 4\).
Biểu diễn nghiệm trên mặt phẳng tọa độ Oxy
- Mỗi nghiệm \(\left( {{x_0};{y_0}} \right)\) của phương trình \(ax + by = c\) được biểu diễn bởi điểm có tọa độ \(\left( {{x_0};{y_0}} \right)\) trên mặt phẳng tọa độ.
- Phương trình bậc nhất hai ẩn \(ax + by = c\) luôn luôn có vô số nghiệm. Tất cả các nghiệm của phương trình đó được biểu diễn bởi một đường thẳng.
Ví dụ:
Nghiệm của phương trình \( - 3x + y = 2\) được biểu diễn bởi đường thẳng d: \(y = 3x + 2\).
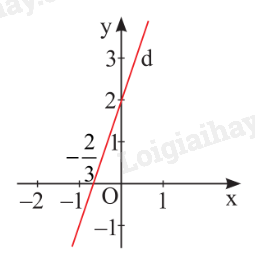
Nghiệm của phương trình \(0x + y = - 2\) được biểu diễn bởi đường thẳng d: \(y = - 2\) vuông góc với Oy tại điểm \(M\left( {0; - 2} \right)\).
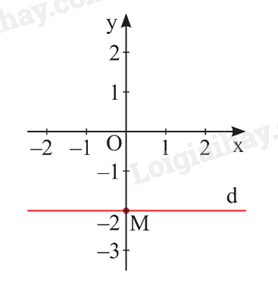
Nghiệm của phương trình \(2x + 0y = 3\) được biểu diễn bởi đường thẳng d: \(x = 1,5\) vuông góc với Ox tại điểm \(N\left( {1,5;0} \right)\).
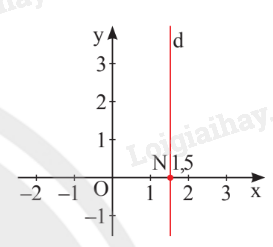
2. Hệ hai phương trình bậc nhất hai ẩn
Khái niệm hệ hai phương trình bậc nhất hai ẩn
|
Hệ hai phương trình bậc nhất hai ẩn x, y có dạng: \(\left\{ \begin{array}{l}ax + by = c\,\,\,\,\,\,\,\,\,(1)\\a'x + b'y = c'\,\,(2)\end{array} \right.\,\,\,\) Trong đó a, b, c, a’, b’, c’ là các số đã biết (gọi là hệ số), \(a \ne 0\) hoặc \(b \ne 0\), \(a' \ne 0\) hoặc \(b' \ne 0\). |
Ví dụ: Hệ phương trình \(\left\{ \begin{array}{l}2x - y = 0\\x + y = 3\end{array} \right.\), \(\left\{ \begin{array}{l}3x = 1\\x - y = 3\end{array} \right.\), \(\left\{ \begin{array}{l}4x - y = 3\\3y = 6\end{array} \right.\) là các hệ phương trình bậc nhất hai ẩn.
Nghiệm của hệ hai phương trình bậc nhất hai ẩn
|
Nếu \(\left( {{x_0};{y_0}} \right)\) là nghiệm chung của hai phương trình (1) và (2) thì \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của hệ. Giải hệ phương trình là tìm tất cả các nghiệm của hệ phương trình đó. |
Ví dụ: Cặp số (1; 2) là một nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x - y = 0\\x + y = 3\end{array} \right.\), vì:
\(2x - y = 2.1 - 2 = 0\) nên (1; 2) là nghiệm của phương trình thứ nhất.
\(x + y = 1 + 2 = 3\) nên (1; 2) là nghiệm của phương trình thứ hai.
