Lý thuyết Khoảng biến thiên và khoảng tứ phân vị Toán 12 Kết nối tri thức
1. Khoảng biến thiên
1. Khoảng biến thiên
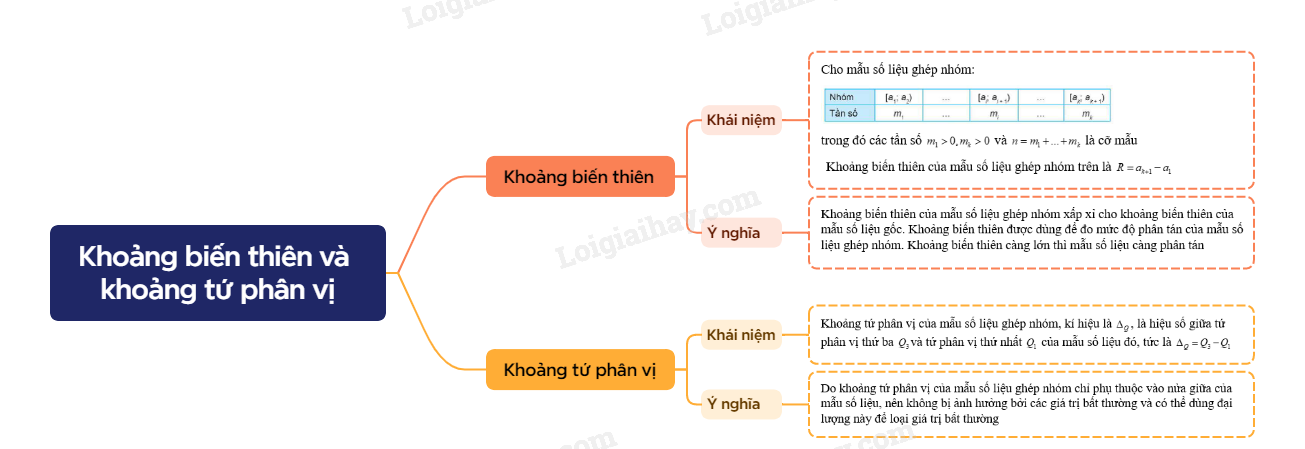
Cho mẫu số liệu ghép nhóm:

trong đó các tần số \({m_1} > 0,{m_k} > 0\) và \(n = {m_1} + ... + {m_k}\) là cỡ mẫu
|
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là \(R = {a_{k + 1}} - {a_1}\) |
Ý nghĩa: Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc. Khoảng biến thiên được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán
2. Khoảng tứ phân vị
|
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là \({\Delta _Q}\), là hiệu số giữa tứ phân vị thứ ba \({Q_3}\)và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\) |
Ý nghĩa: Do khoảng tứ phân vị của mẫu số liệu ghép nhóm chỉ phụ thuộc vào nửa giữa của mẫu số liệu, nên không bị ảnh hưởng bởi các giá trị bất thường và có thể dùng đại lượng này để loại giá trị bất thường