Lý thuyết Mệnh đề - SGK Toán 10 Chân trời sáng tạo
1. Mệnh đề 2. Mệnh đề chứa biến 3. Mệnh đề phủ định
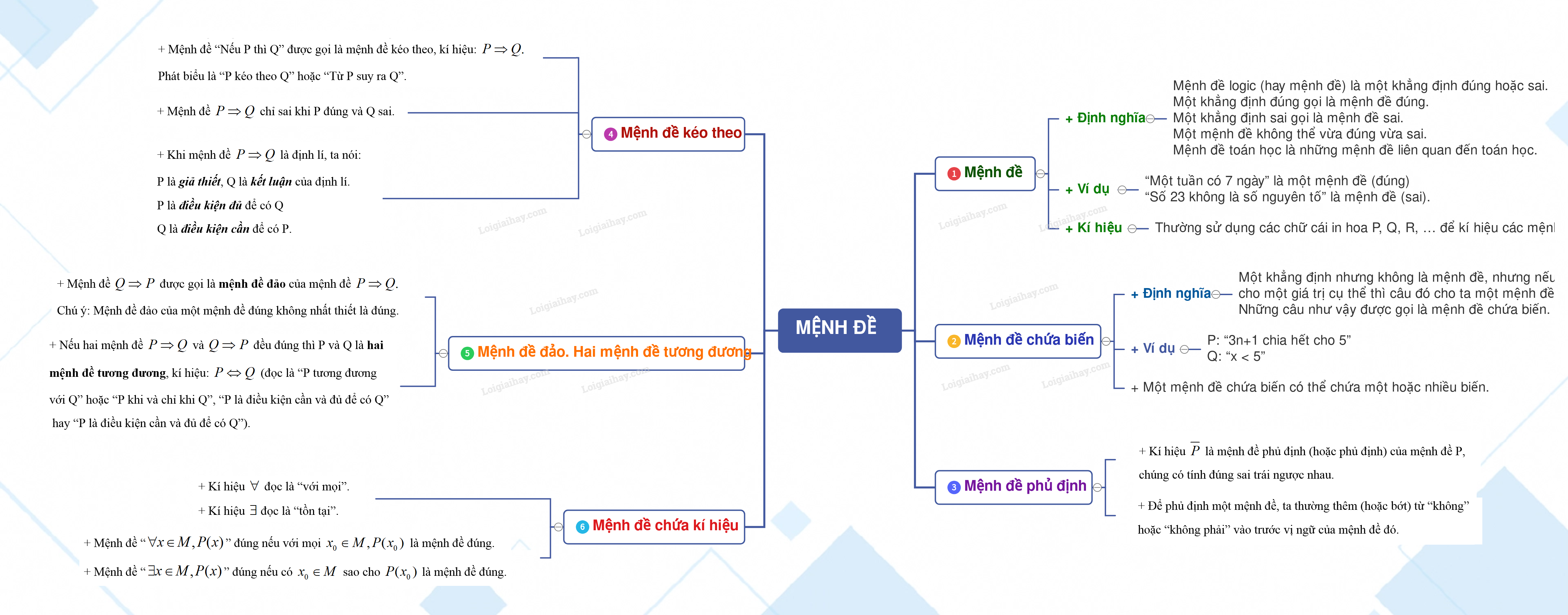
1. Mệnh đề
+ Định nghĩa:
Mệnh đề logic (hay mệnh đề) là một khẳng định đúng hoặc sai.
Một khẳng định đúng gọi là mệnh đề đúng .
Một khẳng định sai gọi là mệnh đề sai .
Một mệnh đề không thể vừa đúng vừa sai.
Mệnh đề toán học là những mệnh đề liên quan đến toán học.
+ Ví dụ:
“Một tuần có 7 ngày” là một mệnh đề (đúng)
“Số 23 không là số nguyên tố” là mệnh đề (sai).
+ Kí hiệu: Thường sử dụng các chữ cái in hoa P, Q, R, … để kí hiệu các mệnh đề.
2. Mệnh đề chứa biến
+ Một khẳng định nhưng không là mệnh đề, nhưng nếu cho một giá trị cụ thể thì câu đó cho ta một mệnh đề. Những câu như vậy được gọi là mệnh đề chứa biến .
Ví dụ: P: “3n+1 chia hết cho 5”
Q: “x < 5”
+ Một mệnh đề chứa biến có thể chứa một hoặc nhiều biến.
3. Mệnh đề phủ định
+ Kí hiệu \(\overline P \) là mệnh đề phủ định (hoặc phủ định) của mệnh đề P, chúng có tính đúng sai trái ngược nhau.
+ Để phủ định một mệnh đề, ta thường thêm (hoặc bớt) từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề đó.
4. Mệnh đề kéo theo
+ Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, kí hiệu: \(P \Rightarrow Q.\) Phát biểu là “P kéo theo Q” hoặc “Từ P suy ra Q”.
+ Mệnh đề \(P \Rightarrow Q\) chỉ sai khi P đúng và Q sai.
+ Khi mệnh đề \(P \Rightarrow Q\) là định lí, ta nói:
P là giả thiết , Q là kết luận của định lí.
P là điều kiện đủ để có Q
Q là điều kiện cần để có P.
5. Mệnh đề đảo. Hai mệnh đề tương đương
+ Mệnh đề \(Q \Rightarrow P\) được gọi là mệnh đề đảo của mệnh đề \(P \Rightarrow Q.\)
Chú ý: Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.
+ Nếu hai mệnh đề \(P \Rightarrow Q\) và \(Q \Rightarrow P\) đều đúng thì P và Q là hai mệnh đề tương đương , kí hiệu: \(P \Leftrightarrow Q\) (đọc là “P tương đương với Q” hoặc “P khi và chỉ khi Q”, “P là điều kiện cần và đủ để có Q” hay “P là điều kiện cần và đủ để có Q”).
6. Mệnh đề chứa kí hiệu \(\forall ,\exists \)
+ Kí hiệu \(\forall \) đọc là “với mọi”.
+ Kí hiệu \(\exists \) đọc là “tồn tại”.
Ví dụ:
“Mọi số thực đều có bình phương lớn hơn 2” viết là: “\(\forall x \in \mathbb{R}|{x^2} > 2\)”
“Có một số thực có bình phương nhỏ hơn 2” viết là: “\(\exists \;x \in \mathbb{R}|{x^2} < 2\)”
+ Mệnh đề “\(\forall x \in M,P(x)\)” đúng nếu với mọi \({x_0} \in M,P({x_0})\) là mệnh đề đúng.
+ Mệnh đề “\(\exists x \in M,P(x)\)” đúng nếu có \({x_0} \in M\) sao cho \(P({x_0})\) là mệnh đề đúng.