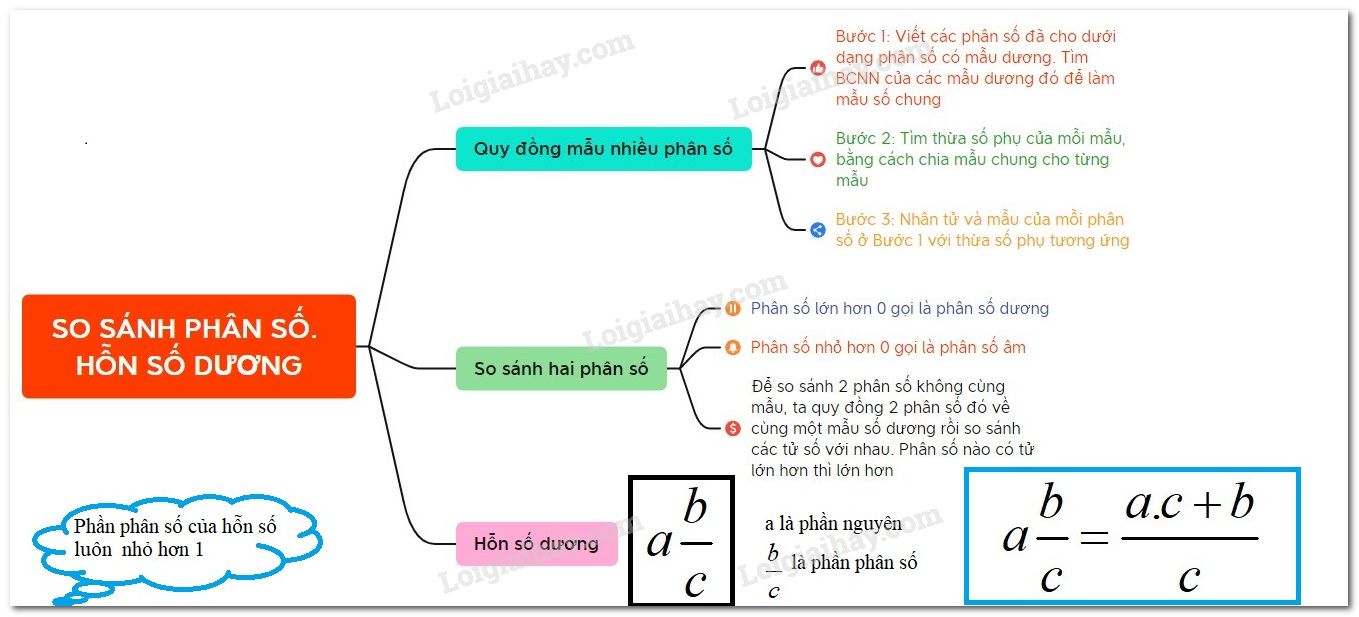
Lý thuyết So sánh phân số. Hỗn số dương Toán 6 Cánh diều
Lý thuyết So sánh phân số. Hỗn số dương Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1. So sánh các phân số:
Trong 2 phân số khác nhau luôn có một phân số lớn hơn phân số kia
*Phân số lớn hơn 0 gọi là phân số dương
*Phân số nhỏ hơn 0 gọi là phân số âm
*Nếu phân số \(\frac{a}{b}\) nhỏ hơn phân số \(\frac{c}{d}\) thì ta viết \(\frac{a}{b}< \frac{c}{d}\) hay \(\frac{c}{d}> \frac{a}{b}\)
*Nếu \(\frac{a}{b}< \frac{c}{d}\) và \(\frac{c}{d}< \frac{e}{g}\) thì \(\frac{a}{b}< \frac{e}{g}\)
a) So sánh hai phân số cùng mẫu
Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.
Ví dụ : So sánh $\dfrac{{ - 4}}{5}$ và $\dfrac{{ - 7}}{5}$.
Ta có: $ - 4 > - 7$ và $5 > 0$ nên $\dfrac{{ - 4}}{5} > \dfrac{{ - 7}}{5}$.
Chú ý : Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.
Ví dụ:
So sánh $\dfrac{{ - 4}}{{ - 5}}$ và $\dfrac{2}{{ - 5}}$
Đưa hai phân số trên về có cùng một mẫu nguyên âm: $\dfrac{4}{5}$ và $\dfrac{{ - 2}}{5}$
Ta có: $4 > - 2$ và $5 > 0$ nên $\dfrac{4}{5} > \dfrac{{ - 2}}{5}$.
b) So sánh hai phân số khác mẫu
Bước 1 : Quy đồng mẫu hai phân số đã cho (về cùng một mẫu dương)
Bước 2 : So sánh tử của các phân số: Phân số nào có tử lớn hơn thì lớn hơn.
Ví dụ : So sánh hai phân số $\dfrac{{ - 7}}{{12}}$ và $\dfrac{{ - 11}}{{18}}$.
$BCNN(12;18) = 36$ nên ta có:
$\dfrac{{ - 7}}{{12}} = \dfrac{{ - 7.3}}{{12.3}} = \dfrac{{ - 21}}{{36}}$
$\dfrac{{ - 11}}{{18}} = \dfrac{{ - 11.2}}{{18.2}} = \dfrac{{ - 22}}{{36}}$.
Vì $ - 21 > - 22$ nên $\dfrac{{ - 21}}{{36}} > \dfrac{{ - 22}}{{36}}$. Do đó $\dfrac{{ - 7}}{{12}} > \dfrac{{ - 11}}{{18}}$.
c) Áp dụng quy tắc so sánh phân số
Phân số có tử và mẫu là hai số nguyên cùng dấu thì lớn hơn $0$ , gọi là phân số dương.
Ví dụ : $\dfrac{{ - 3}}{{ - 5}} > 0$ hoặc $\dfrac{4}{5} > 0$
Phân số có tử và mẫu là hai số nguyên khác dấu thì nhỏ hơn $0$, gọi là phân số âm.
Ví dụ : $\dfrac{{ - 3}}{5} < 0$
- Ta còn có các cách so sánh phân số như sau:
+ Áp dụng tính chất: $\dfrac{a}{b} < \dfrac{c}{d} \Leftrightarrow a.d < b.c{\rm{\;}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in {\rm{Z}};{\rm{b}},{\rm{d\;}} > {\rm{\;0}})$
+ Đưa về hai phân số cùng tử dương rồi so sánh mẫu (chỉ áp dụng đối với hai phân số cùng âm hoặc cùng dương)
Ví dụ : $\dfrac{4}{{ - 9}} > \dfrac{4}{{ - 7}};$$\dfrac{3}{5} < \dfrac{3}{2}$
+ Chọn số thứ ba làm trung gian.
Ví dụ:
$\dfrac{{ - 4}}{9} < 0 < \dfrac{4}{7}{\kern 1pt}$ suy ra $\dfrac{{ - 4}}{9}<\dfrac{4}{7}$
$\dfrac{{14}}{9} > 1 > \dfrac{4}{7}$ suy ra $\dfrac{{14}}{9}>\dfrac{4}{7}$
+ Sử dụng tính chất so sánh: Nếu \(\dfrac{a}{b} < 1\) thì \(\dfrac{a}{b} < \dfrac{{a + m}}{{b + m}}\)
2. Hỗn số dương
Viết một phân số lớn hơn 1 thành tổng của một số nguyên dương và một phân số nhỏ hơn 1 ( với tử và mẫu dương) rồi viết chúng liền nhau thì được 1 hỗn số dương.
Ví dụ:
\(\frac{7}{4}= \frac{4.1+3}{4}= 1 + \frac{3}{4}=1\frac{3}{4}\)