Lý thuyết Số nguyên âm Toán 6 Cánh diều
Lý thuyết Số nguyên âm Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
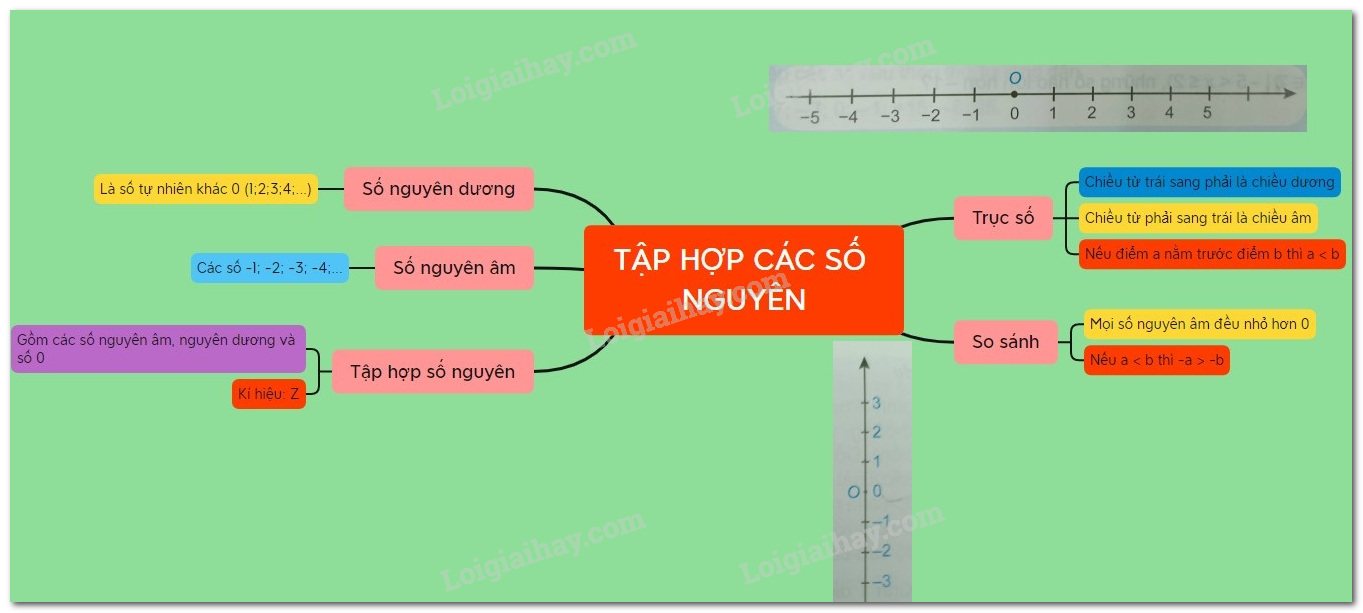
Số nguyên dương: \(1;2;3;4;...\) (Số tự nhiên khác 0)
Số nguyên âm: \(- 1; - 2; - 3; - 4;...\)(Ta thêm dấu “-” vào đằng trước các số nguyên dương)
- Tập hợp: \(\left\{ {...; - 3; - 2; - 1;0;1;2;3;...} \right\}\) gồm các số nguyên âm, số \(0\) và các số nguyên dương là tập hợp các số nguyên . Kí hiệu là \(\mathbb{Z} = \left\{ {...; - 3; - 2; - 1;0;1;2;3;...} \right\}\)
Chú ý :
- Số \(0\) không phải là số nguyên dương cũng không phải số nguyên âm.
- Đôi khi ta còn viết thêm dấu “+” ngay trước một số nguyên dương. Chẳng hạn \( + 5\) (đọc là “dương năm”)
Khi nào người ta dùng số âm?
- Trong đời sống hàng ngày người ta dùng các số mang dấu "-" và dấu "+" để chỉ các đại lượng có thể xét theo hai chiều khác nhau.
|
Số dương biểu thị |
Số âm biểu thị |
|
Nhiệt độ trên \({0^0}C\) |
Nhiệt độ dưới \({0^0}C\) |
|
Độ cao trên mực nước biển |
Độ cao dưới mực nước biển |
|
Số tiền hiện có |
Số tiền còn nợ |
|
Số tiền lãi |
Số tiền lỗ |
|
Độ viễn thị |
Độ cận thị |
Ví dụ :
+) Số \( - 1\) đọc là “âm một”.
+) Số +2 đọc là “dương hai”
+) Một người thợ lặn lặn xuống độ sâu 10 mét tức là độ cao hiện tại của người thợ lặn là -10m so với mực nước biển.